SM4代码实现

算法过程

更多的原理介绍参考：SM4原理介绍

代码实现

S盒实现

#include <stdio.h>
/*
    SM4-S盒实现：
    由三个复合函数组成，S(x)=L(I(L(x)))，其中L(x)是仿射变换，而I(x)是逆变换
*/
int sbox[256]; // S盒

//仿射变换实现
int change(int x)
{
    int A1 = 0xA7;
    int flag;
    int result = 0;
    int tem;
    int flage2;
    for (int i = 0; i < 8; i++)
    {
        flag = (A1 & 0x80) >> 7;
        tem = x & A1;
        flage2 = 0;
        for (int j = 0; j < 8; j++)
        {
            flage2 ^= (tem & 1);
            tem >>= 1;
        }
        result = result | (flage2 << i);
        A1 = (A1 << 1) | flag;
    }
    result ^= 0xd3;
    return result;
}

//模2 多项式乘法
int multiplication(int a, int b)
{
    int tem = 0;
    int i = 0;
    while (b)
    {
        if (b & 1)
        {
            tem ^= a << i;
        }
        i++;
        b >>= 1;
    }
    return tem;
}

//模2 多项式除法
int length(int x)
{
    int i = 0;
    int comp = 1;
    while (1)
    {
        if (comp >= x)
        {
            return i;
        }
        comp = (comp << 1) + 1;
        i++;
    }
}
void division(int a, int b, int* round, int* left)
{
    *round = 0;
    *left = 0;
    int distence;
    while (1)
    {
        distence = length(a) - length(b);
        if (distence >= 0 && a)
        {
            a = a ^ (b << distence);
            *round = (*round) | (1 << distence);
        }
        else {
            *left = a;
            break;
        }
    }
}

//模2 多项式求逆（扩展欧几里得算法）
int inverse(int a, int b)
{
    int x2 = 1;
    int x1 = 0;
    int y2 = 0;
    int y1 = 1;
    int temX1, temY1;
    int q, r, x, y;
    int i;
    while (b)
    {
        division(a, b, &q, &r);
        y = y2 ^ multiplication(q, y1);

        a = b;
        b = r;
        y2 = y1;
        y1 = y;
    }
    return y2;
}

void genXbox()
{
    printf("-------------------------------------------------------------SM4-Sbox生成---------------------------------------------------------\n");
    for (int i = 0; i <= 0xf; i++)
    {
        printf("\t%x", i);
    }
    printf("\n");
    for (int i = 0; i <= 0xf; i++)
    {
        printf("%x", i);
        for (int j = 0; j <= 0xf; j++)
        {
            printf("\t%x", change(inverse(0x1f5, change((i << 4) | j))));
        }
        printf("\n");
    }
    printf("----------------------------------------------------------------------------------------------------------------------------------\n");
    system("pause");

}

int main()
{
    genXbox();
    return 0;
}

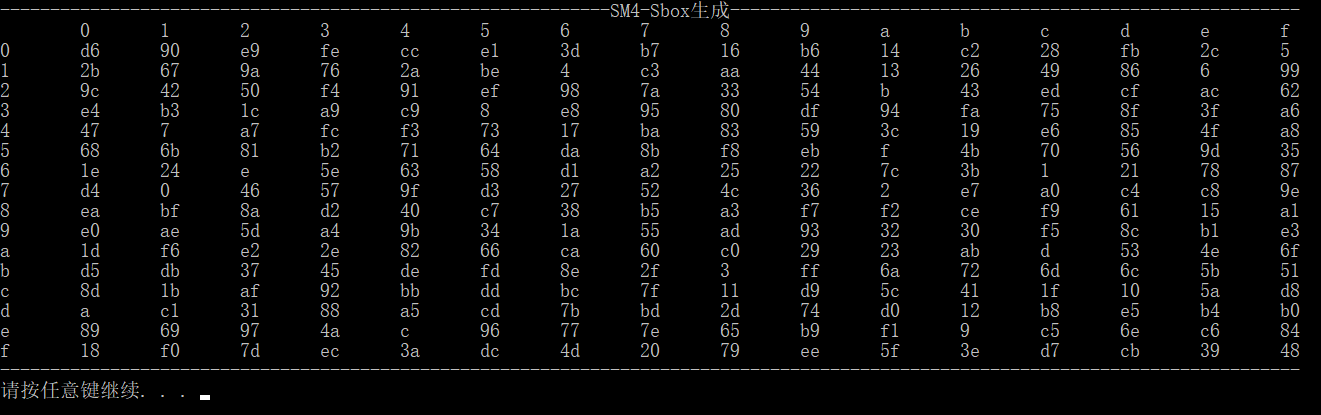
以上是S盒实现，详细代码见github

后续可实现：txt文本加密、Doc文件加密、图片加密、PDF文本加密

参考

1、国标—SM4

2、密码学-基础理论与应用（李子臣著）

3、商用密码检测中心-源码下载