POJ 3352 Road Construction(边双连通分量，桥，tarjan)

题解转自http://blog.csdn.net/lyy289065406/article/details/6762370   文中部分思路或定义模糊，重写的红色部分为修改过的。

大致题意：

　　某个企业想把一个热带天堂岛变成旅游胜地，岛上有N个旅游景点，保证任意2个旅游景点之间有路径连通的（可间接连通）。而为了给游客提供更方便的服务，该企业要求道路部门在某些道路增加一些设施。

　　道路部门每次只会选择一条道路施工，在该条道路施工完毕前，其他道路依然可以通行。然而有道路部门正在施工的道路，在施工完毕前是禁止游客通行的。这就导致了在施工期间游客可能无法到达一些景点。

　　为了在施工期间所有旅游景点依然能够正常对游客开放，该企业决定搭建一些临时桥梁，使得不管道路部门选在哪条路进行施工，游客都能够到达所有旅游景点。给出当下允许通行的R条道路，问该企业至少再搭建几条临时桥梁，才能使得游客无视道路部门的存在到达所有旅游景点？

　　题目所给的图是连通的，且所给的边没有重复的，所以不考虑重边。

　　 注意：不要把Sample Input 1读入，更不要把它输出！！！！！

首先建立模型：

给定一个连通的无向图G，至少要添加几条边，才能使其变为边-双连通图（因为在修道路是一条边！）。

模型很简单，正在施工的道路我们可以认为那条边被删除了。那么一个图G能够在删除任意一条边后，仍然是连通的，当且仅当图G至少为边双连通的。

PS：不要问我为什么不是3-连通、4-连通...人家题目问“至少添加几条边”好不...

显然，当图G存在桥（割边）的时候，它必定不是边双连通的。桥的两个端点必定分别属于图G的两个【边双连通分量】（注意不是点双连通分量），一旦删除了桥，这两个【边双连通分量】必定断开，图G就不连通了。但是如果在两个【边双连通分量】之间再添加一条边，桥就不再是桥了，这两个【边双连通分量】之间也就是边双连通了。

那么如果图G有多个【边双连通分量】呢？至少应该添加多少条边，才能使得任意两个【边双连通分量】之间都是边双连通的（也就是图G是边双连通的）？

这个问题就是本题的问题。要解决这个问题：

1、  首先要找出图G的所有【边双连通分量】。

Tarjan算法用来寻找图G的所有【边双连通分量】是最简单有效的方法，因为Tarjan算法在DFS过程中会对图G所有的结点都生成一个Low值，而由于题目已表明任意两个结点之间不会出现重边，因此Low值相同的两个结点必定在同一个【边双连通分量】中（但是！！low值不同的点并不代表就不在同一个边双连通分量中，因为由于先后访问的顺序的原因，low值可能会不同，这跟并查集的道理是一样的，如果不进行压缩路径，几乎很多人的直接上级都不会是该团队的boss，这点可以模仿并查集的方式将其归到只有两层，查起来就很快了，否则可能超时！！当然你不考虑这点也能AC，水果了那些简单数据，但是下面这2组数据你可能过不了）！

11 14
1 2
1 3
1 4
2 5
6 11
2 6
5 6
5 11
3 7
3 8
7 8
4 9
4 10
9 10

11 14
1 2
1 3
1 4
5 11
2 5
2 6
5 6
6 11
3 7
3 8
7 8
4 9
4 10
9 10

以上两个测试数据的ans都是2。

2、  把每一个【边双连通分量】都看做一个点（即【缩点】）

也有人称【缩点】为【块】，都是一样的。其实缩点不是真的缩点，只要利用Low值对图G的点分类处理，就已经缩点了。

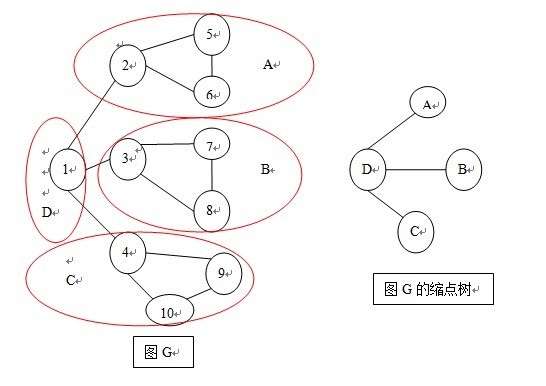
以样例1为例，样例1得到的图G为上左图，

其中Low[4]=Low[9]=Low[10]

Low[3]=Low[7]=Low[8]

Low[2]=Low[5]=Low[6]

Low[1]独自为政....

把Low值相同的点划分为一类，每一类就是一个【边双连通分量】，也就是【缩点】了，不难发现，连接【缩点】之间的边，都是图G的桥，那么我们就得到了上右图以缩点为结点，以桥为树边所构造成的树。

　　以上这样以low值判断边连通分量是没有错的！只是要确保low值能区分出该块，当然，你可以用栈，就像求点双连通分量那样（并不是完全一样，那是以割点来区分的，这是以桥来区分的）。

3、  问题再次被转化为“至少在缩点树上增加多少条树边，使得这棵树变为一个边双连通图”。

首先知道一条等式：

若要使得任意一棵树，在增加若干条边后，变成一个双连通图，那么

至少增加的边数 =（ 这棵树总度数为1的结点数 + 1 ）/ 2

（证明就不证明了，自己画几棵树比划一下就知道了）

那么我们只需求缩点树中总度数为1的结点数（不一定是叶子数，如果树根仅有1个孩子，同样要将其统计进来）有多少就可以了。换而言之，我们只需求出所有缩点的度数，然后判断度数为1的缩点有几个，问题就解决了。

4、  求出所有缩点的度数的方法

两两枚举图G的直接连通的点（如果求出了桥，那么枚举桥也行的，相同于直接枚举树的边），只要这两个点不在同一个【缩点】中，那么它们各自所在的【缩点】的度数都+1。注意由于图G时无向图，这样做会使得所有【缩点】的度数都是真实度数的2倍，必须除2后再判断是否度为1。

特别注意：求【点双连通分量】与【边双连通分量】是不同的模板，勿混淆。

 #include <iostream>
 #include <cmath>
 #include <cstdio>
 #include <vector>
 #include <cstring>
 #include <set>
 //#include <bits/stdc++.h>
 using namespace std;
 const int N=+;
 vector<int> vect[N];
 int low[N], dfn[N],  cnter;
 int du[N];
 int pre[N];//这个与dfn是相反的索引
 vector<pair<int,int> >  cutt;
 int find(int x) //寻找x的low值
 {
     if(low[x]==dfn[x])  return low[x];
     return low[x]=find( pre[low[x] ] );
 }

 void DFS(int x, int far)
 {
     low[x]= dfn[x]= ++cnter;
     pre[cnter]=x;   //标记第cnter个访问的是谁
     for(int i=; i<vect[x].size(); i++)
     {
         int t=vect[x][i];
         if(!dfn[t])
         {
             DFS(t,x);
             low[x]=min(low[x],low[t]);
             if(low[t]>dfn[x])   cutt.push_back(make_pair(x,t));//桥（即树边）
         }
         else if(t!=far)    low[x]=min(low[x],dfn[t]);
     }
 }

 int cal_bcc(int f)
 {
     cutt.clear();
     memset(du,,sizeof(du));
     memset(low,,sizeof(low));
     memset(dfn,,sizeof(dfn));
     memset(pre,,sizeof(pre));
     cnter=;
     DFS(,);
     for(int i=; i<cutt.size(); i++)
     {
         int a=cutt[i].first;
         int b=cutt[i].second;
         du[find(a)]++;
         du[find(b)]++;
     }

     int ans=;
     for(int i=; i<=f; i++)    if(du[i]==)    ans++;
     return ((ans+)/);
 }

 int main()
 {
     //freopen("input.txt", "r", stdin);
     int f, r, a, b, j=;
     char s[N];
     while(cin>>f>>r)
     {
         for(int i=; i<=f; i++) vect[i].clear();
         while(r--)
         {
             scanf("%d%d", &a, &b);
             vect[a].push_back(b);
             vect[b].push_back(a);
         }
         printf("%d\n",cal_bcc(f));
     }
     return ;
 }

AC代码