矩阵LU分解
有如下方程组 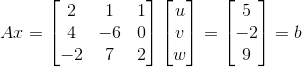 ,当矩阵 A 各列向量互不相关时, 方程组有位移解,可以使用消元法求解,具体如下:
,当矩阵 A 各列向量互不相关时, 方程组有位移解,可以使用消元法求解,具体如下:
使用消元矩阵将 A 变成上三角矩阵 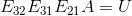 ,
,
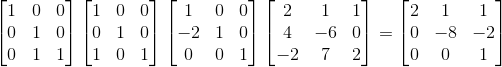 ,
,
使用消元矩阵作用于向量 b,得到向量 c,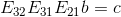 ,
,
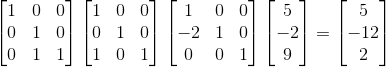 ,
,
Ax=b 消元后变为 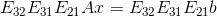 ,即
,即 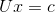 , 由于
, 由于  为上三角矩阵, 使用回带法即可求解方程组。
为上三角矩阵, 使用回带法即可求解方程组。
对矩阵 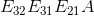 做如下运算
做如下运算 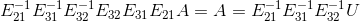 。在消元过程中,已知
。在消元过程中,已知 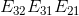 ,如何求解
,如何求解 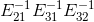 呢?
呢?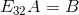 表示将矩阵A的第二行乘以 1 再加上矩阵A的第三行得到矩阵B的第三行,矩阵B的第一二行于矩阵A的第一二行保持一致。根据语义,
表示将矩阵A的第二行乘以 1 再加上矩阵A的第三行得到矩阵B的第三行,矩阵B的第一二行于矩阵A的第一二行保持一致。根据语义,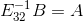 表示将矩阵B的第二行乘以 -1 再加上矩阵B的第三行得到矩阵A的第三行,矩阵A的第一二行于矩阵B的第一二行保持一致。
表示将矩阵B的第二行乘以 -1 再加上矩阵B的第三行得到矩阵A的第三行,矩阵A的第一二行于矩阵B的第一二行保持一致。
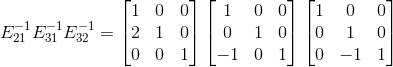 ,
,
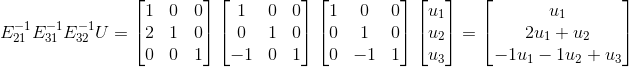 ,
,
通过以上观察,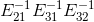 仅需将对角线下元素相加即可得到,
仅需将对角线下元素相加即可得到,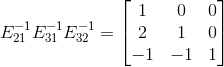 ,在矩阵消元过程中,对消元系数取反,然后放在相应的位置即构成了
,在矩阵消元过程中,对消元系数取反,然后放在相应的位置即构成了 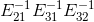 ,也就是 L 。同时,消元法记录下了 U,则有 Ux=c, b=Lc。
,也就是 L 。同时,消元法记录下了 U,则有 Ux=c, b=Lc。
由于 L 为下三角矩阵,根据 Lc=b, 可求解 c;U 为上三角矩阵, 根据 Ux=c 可求解 x。
在消元过程中,如果遇到主元位置上为 0 情况时,需要使用行变换矩阵使消元过程得以继续,PAx=Pb,P为行变换矩阵,记录矩阵 L,U,P,可实现LU分解,过程如下:
有方程组 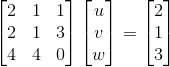 ,对矩阵
,对矩阵 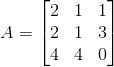 进行LU分解:
进行LU分解:
1)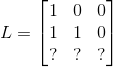 ,
, 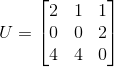 ,
,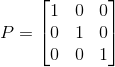 ;
;
2)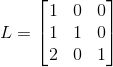 ,
,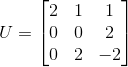 ,
,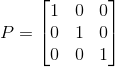 ;
;
3)由于 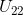 为 0,需要交换2,3行,则有:
为 0,需要交换2,3行,则有:
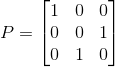 ,
, 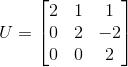 ,
,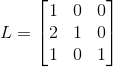 ,交换L矩阵中小于第二列下变换因子位置,即交换
,交换L矩阵中小于第二列下变换因子位置,即交换 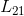 与
与  元素位置;
元素位置;
4)由于 Lc=Pb, 可计算出 c:
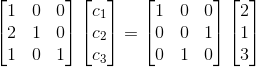 ,
, 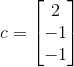 ;
;
5)由于 Ux=c,可计算出 x:
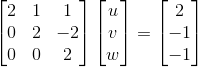 ,
,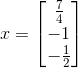 。
。
参考资料 Linear Algebra And Its Applications Gilbert Strang
矩阵LU分解的更多相关文章
- 矩阵LU分解的MATLAB与C++实现
一:矩阵LU分解 矩阵的LU分解目的是将一个非奇异矩阵\(A\)分解成\(A=LU\)的形式,其中\(L\)是一个主对角线为\(1\)的下三角矩阵:\(U\)是一个上三角矩阵. 比如\(A= \beg ...
- 矩阵LU分解分块算法实现
本文主要描述实现LU分解算法过程中遇到的问题及解决方案,并给出了全部源代码. 1. 什么是LU分解? 矩阵的LU分解源于线性方程组的高斯消元过程.对于一个含有N个变量的N个线性方程组,总可以用高斯消去 ...
- 矩阵LU分解程序实现(Matlab)
n=4;%确定需要LU分解的矩阵维数 %A=zeros(n,n); L=eye(n,n);P=eye(n,n);U=zeros(n,n);%初始化矩阵 tempU=zeros(1,n);tempP=z ...
- 计算方法 -- 解线性方程组直接法(LU分解、列主元高斯消元、追赶法)
#include <iostream> #include <cstdio> #include <algorithm> #include <cstdlib> ...
- MATLAB矩阵的LU分解及在解线性方程组中的应用
作者:凯鲁嘎吉 - 博客园http://www.cnblogs.com/kailugaji/ 三.实验程序 五.解答(按如下顺序提交电子版) 1.(程序) (1)LU分解源程序: function [ ...
- 线性代数笔记10——矩阵的LU分解
在线性代数中, LU分解(LU Decomposition)是矩阵分解的一种,可以将一个矩阵分解为一个单位下三角矩阵和一个上三角矩阵的乘积(有时是它们和一个置换矩阵的乘积).LU分解主要应用在数值分析 ...
- 矩阵分解---QR正交分解,LU分解
相关概念: 正交矩阵:若一个方阵其行与列皆为正交的单位向量,则该矩阵为正交矩阵,且该矩阵的转置和其逆相等.两个向量正交的意思是两个向量的内积为 0 正定矩阵:如果对于所有的非零实系数向量x ,都有 x ...
- 第五节、矩阵分解之LU分解
一.A的LU分解:A=LU 我们之前探讨过矩阵消元,当时我们通过EA=U将A消元得到了U,这一节,我们从另一个角度分析A与U的关系 假设A是非奇异矩阵且消元过程中没有行交换,我们便可以将矩阵消元的EA ...
- matlab 求解线性方程组之LU分解
线性代数中的一个核心思想就是矩阵分解,既将一个复杂的矩阵分解为更简单的矩阵的乘积.常见的有如下分解: LU分解:A=LU,A是m×n矩阵,L是m×m下三角矩阵,U是m×n阶梯形矩阵 QR分解: 秩分解 ...
随机推荐
- bind 标签
<select id="finduserbylikename" parameterType="string" resultMap="cour ...
- Git 基础指令
Git 基础指令 Git 基础指令 获取 Git 仓库 在已存在目录中初始化仓库 克隆现有的仓库 记录仓库与仓库的更新 仓库的记录 检查当前文件状态 三部曲 跟踪新文件 提交更新 移除文件 推送到远程 ...
- java集合【13】——— Stack源码分析走一波
前言 集合源码分析系列:Java集合源码分析 前面已经把Vector,ArrayList,LinkedList分析完了,本来是想开始Map这一块,但是看了下面这个接口设计框架图:整个接口框架关系如下( ...
- 使用Python 爬取 京东 ,淘宝。 商品详情页的数据。(避开了反爬虫机制)
以下是爬取京东商品详情的Python3代码,以excel存放链接的方式批量爬取.excel如下 代码如下 from selenium import webdriver from lxml import ...
- 手动安装selenium包
1.下载selenium安装包 https://pypi.org/project/selenium 2.解压selenium-3.12.0.tar.gz 3.cmd环境进入到selenium的setu ...
- 【刷题-PAT】A1126 Eulerian Path (25 分)
1126 Eulerian Path (25 分) In graph theory, an Eulerian path is a path in a graph which visits every ...
- 【采坑小计】thanos receiver的官方文档中,并未说明tsdb落盘的配置方式
官方文档的地址在:https://thanos.io/tip/components/receive.md/ 一开始以为落盘的时间间隔是:--tsdb.retention=15d 实际测试中发现,tha ...
- vs python2.7 bug
微软vs里面小细节的bug真他妈的多
- python13day
昨日回顾 生成器:生成器就是迭代器,生成器是自己用python代码构建的 生成器函数 生成器表达式 python内部提供的 如何判断函数和生成器函数 yield yield return 吃包子的区别 ...
- 学习Java第15天
今天所做的工作: 学习了HTML的基本标签,vs code的基本使用 明天工作安排: 继续学习html 目前所遇到的大都是HTML标签数量多,较复杂的问题,继续找规律记忆吧.
