【LeetCode】931. Minimum Falling Path Sum 解题报告（Python）

作者：负雪明烛
id： fuxuemingzhu
个人博客： http://fuxuemingzhu.cn/

题目描述

Given a square array of integers A, we want the minimum sum of a falling path through A.

A falling path starts at any element in the first row, and chooses one element from each row. The next row’s choice must be in a column that is different from the previous row’s column by at most one.

Example 1:

Input: [[1,2,3],[4,5,6],[7,8,9]]

Output: 12

Explanation:

The possible falling paths are:

[1,4,7], [1,4,8], [1,5,7], [1,5,8], [1,5,9]
[2,4,7], [2,4,8], [2,5,7], [2,5,8], [2,5,9], [2,6,8], [2,6,9]
[3,5,7], [3,5,8], [3,5,9], [3,6,8], [3,6,9]

The falling path with the smallest sum is [1,4,7], so the answer is 12.

Note:

1 <= A.length == A[0].length <= 100
-100 <= A[i][j] <= 100

题目大意

从最上面一行开始向下走，每次移动的时候最多只可以移动一列。也就是说每次必须向下走一行，列可以不变、也可以向左右移动一列。求到达最后一行的时候，最短的路径长度。

解题方法

动态规划

刚做过类似的题目，但是我还是没有做出来。。这个题和799香槟塔很像，都是二维空间求最大、最小的路径问题。

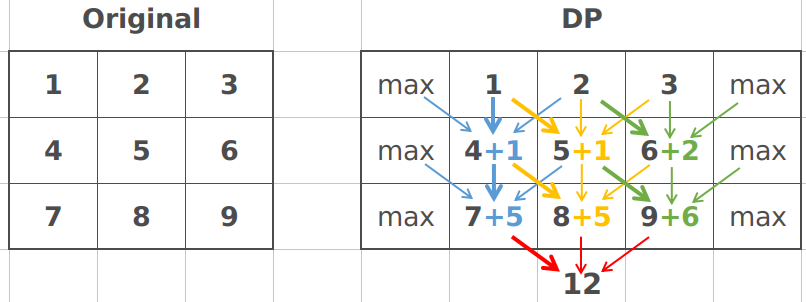
如果看上面这个图就明白了，数组中每个位置都要从上一层获得三个相邻列的最小值，换句话说，每个位置都可以给下面三个相邻列传递最小值。那么，其实就是一个动态规划嘛，到每个位置的最短路径，就是当前数值加上到达上面那层的三个相邻列的最小值。

所以这个题代码其实很简单，只需要设置好边界，然后我们每次查找上面的三个最小值加上当前的位置，得到的就是到达当前位置的最小路径。

做DP的时候，不要怕设置边界条件。我以前总想着用各种方法想着让dp数组和原来的数组一样大，这个思想是错误的！因为我们记忆化搜索的时候实际上有很多边界条件的，其实是可以转化成dp的边界条件，或者说是初始条件。提前给dp数组设定各种边界条件，能简化很多状态转移代码～这个题就很好的说明了这点！

时间复杂度是O(MN)，空间复杂度是O(MN)。

class Solution(object):

    def minFallingPathSum(self, A):

        """

        :type A: List[List[int]]

        :rtype: int

        """

        M, N = len(A), len(A[0])

        dp = [[0] * (N + 2) for _ in range(M)]

        for i in range(M):

            dp[i][0] = dp[i][-1] = float('inf')

            for j in range(1, N + 1):

                dp[i][j] = A[i][j - 1]

        for i in range(1, M):

            for j in range(1, N + 1):

                dp[i][j] = A[i][j - 1] + min(dp[i - 1][j - 1], dp[i - 1][j], dp[i - 1][j + 1])

        return min(dp[-1])

相似题目

799. Champagne Tower
【面试现场】如何编程获得最多的年终红包奖？

参考资料

https://leetcode.com/problems/minimum-falling-path-sum/discuss/186689/Java-DP-solution-with-graph-illustrated-explanations

日期

2018 年 10 月 28 日 —— 啊，悲伤的周赛