LCD RGB 控制技术讲解 — 时钟篇（上）【转】

1. 时序图

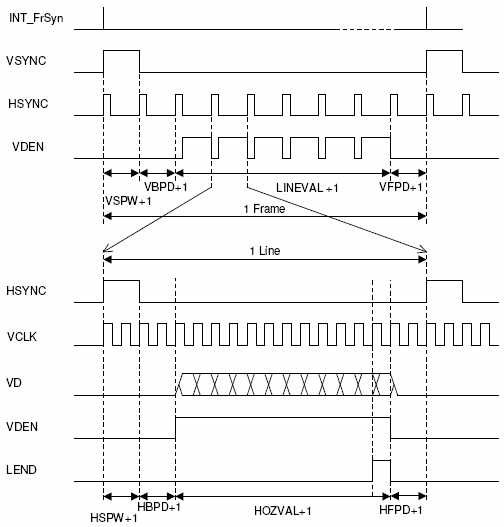
下面是LCD RGB 控制的典型时序图

天啊，一下就上这玩意，怎么看？？？

其实要解释上面的时序图，我们还需要了解一些LCD的显示过程。所以现在只是有个印象，稍后我们详细讲解。

2. LCD显示流程

LCD显示一张图片，其实是每一个像素点的填充，只是速度很快我们人眼没有察觉而已。如果将LCD的显示频率降低，我们能明显感觉整个屏幕的闪烁现象。

我们将LCD屏幕分为水平方向和垂直方向

一般我们的行在水平方向，LCD每一行的像素点被逐一填充，填充完一行继续填充下一行，填充顺序可以为左->右或者右->左

一行有多少像素点？

一个LCD需要填充多少行？

通过查看LCD的手册，例如一个800*480的液晶屏，表示一行（水平）800个像素点，一共有480行。

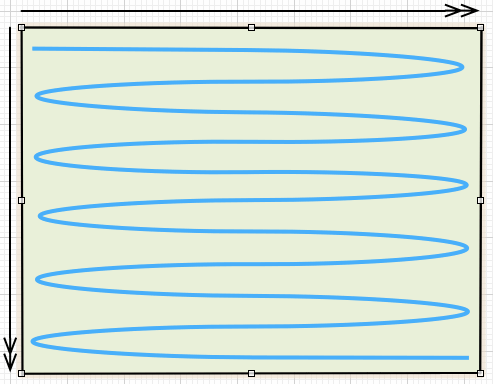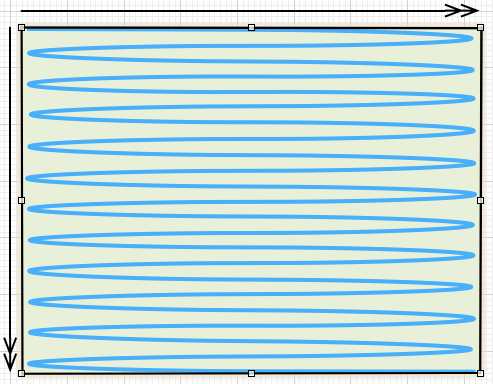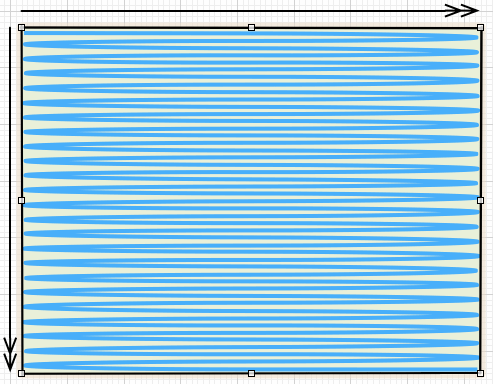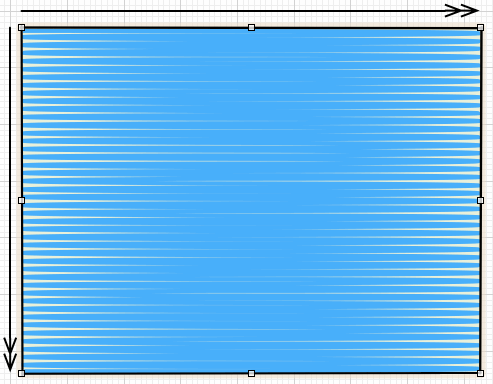
例如下图中现实一帧的图像(从左到右，从上到下)

每一帧图像，就从第一行的第一个像素点一直填充到最后一行的最后一个像素点。

为了能简单演示一下效果，假设我们现在让LCD显示蓝色，那么LCD的填充效果就像下面的图片

好了，如果能了解这个像素填充的过程。那么我接下来就开始分时时钟和LCD显示的关系。

3. LCD时钟分析

我们知道了LCD现实一帧图像也就是像素填充的过程，但是由于速度太快我们察觉不出来，那么这个“快”到底是多快呢？

3.1 显示一行

800*480的RGB LCD屏幕
24bpp 显示模式

显示一行，我们LCD需要填充800个像素点。每一个像素由RGB三元素组成，每个元素(R、G、B)由8bit位数组成，也就是说一个像素我们需要通过信号线传输24bit的数据。
那么显示一行800个像素需要多长时间呢？我们先看一个要介绍的时钟–像素时钟CLK

3.1.1 像素时钟

上图中CLK就是像素时钟，每一个时钟周期发送一个像素的数据。根据我们LCD的参数，例如一行有800个像素，那么经过800个CLK时钟，我们就填充完了800个像素。
问题来了…

哪一个CLK代表一行的开始？
哪一个CLK代表第一个有效的像素数据？

所以针对上面的问题，我们还需要介绍两个时钟行同步时钟HSYNC和有效数据使能VDEN

3.1.2 水平同步时钟 HSYNC

HSYNC水平同步信号，表示一行数据的开始。具体如下图

其中CLK没有任何变化，只是多了HSYNC和DEN两个信号。

如图中的红色箭头，当HSYNC产生了如图所示的变化表示新的一行数据传送马上开始，当ENB信号线为高电平期间传输的数据视为有效数据。这样一来，一行800个像素的数据才能正确的传送完成。

3.2 显示一帧

3.2.1 垂直同步时钟VSYNC

为什么要有VSYNC呢，按照我们之前假设的800*480LCD。从第一行一直到最后一行，整个LCD屏幕所有像素填充完毕，这一过程也就是写了一帧数据，我们如果要LCD能够实时显示画面，很显然一帧数据肯定不够，所以L要给LCD不断的提供新的帧数据，这无非也就是重复上述显示一帧的过程。

上图中VSYNC垂直同步信号，当产生如图所示的变化，就代表新的一帧数据马上开始传送。那么这里没有有效数据信号呢？？

其实很简单，因为新的一帧数据不就是从LCD第一行的第一个像素开始填充嘛，那么前面我们已经说明了每一行都自己的同步信号，而每一行也有对应的数据有效信号线。所以垂直同步信号只用关心从一帧数据(8000*480)的同步，而不同关心每一行的同步。

于是，我们将上面分析的时钟放在一起，就变成了LCD RGB模式的典型时序图

上图中VSYNC垂直同步信号，当产生如图所示的变化，就代表新的一帧数据马上开始传送。那么这里没有有效数据信号呢？？

于是，我们将上面分析的时钟放在一起，就变成了LCD RGB模式的典型时序图