算法问题实战策略 GALLERY

地址 https://algospot.com/judge/problem/read/GALLERY

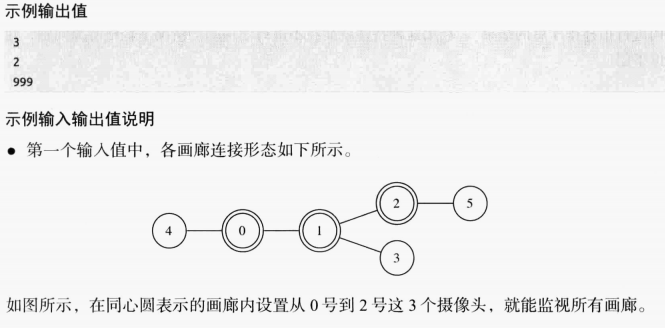
分析

如图 显然是需要在 0 1 2三个点进行监控即可。（0 2 3 也可）

根据题意，不存在回路，也就是不重复经过两画廊之间的走廊是不可能在两画廊之间进行走动的

我们可以将该图看成一棵树，深度优先遍历时，叶子结点的父节点需要放置摄像头，这样能将叶子结点 父节点和父节点的父节点均可监视到。然后根据有无未监视的子节点 决定当前节点的状态(需要放置，被监视，未被监视)

代码如下

 #include <iostream>
 #include <vector>

 using namespace std;

 const int N = ;
 int V;
 vector<int> adj[];
 vector<bool> visited;
 const int UNWATCHED = ;
 const int  WATCHED = ;
 const int INSTALLED = ;

 int installed;

 int dfs(int here)
 {
     visited[here] = true;
     int children[] = { ,, };
     for (int i = ; i < adj[here].size(); i++)
     {
         int there = adj[here][i];
         if (!visited[there])
             ++children[dfs(there)];
     }

     //后代节点存在没有监视的节点 在该节点安装摄像头
     if (children[UNWATCHED]) {
         ++installed;
         return INSTALLED;
     }

     if (children[INSTALLED]) {
         return WATCHED;
     }

     return UNWATCHED;
 }

 int installCamera()
 {
     installed = ;
     visited = vector<bool>(V, false);
     for (int u = ; u < V; ++u) {
         if (!visited[u] && dfs(u) == UNWATCHED)
             ++installed;
     }

     return installed;
 }

 /*
 3
 6 5
 0 1
 1 2
 1 3
 2 5
 0 4
 4 2
 0 1
 2 3
 1000 1
 0 1
 =====================
 3
 2
 999
 */

 int main()
 {
     int sampleCount = ;
     cin >> sampleCount;
     while (sampleCount--) {
         int n, m; visited.clear();
         for (int i = ; i < ; i++) adj[i].clear();
         cin >> V >> m;
         for (int i = ; i < m; i++) {
             int a, b;
             cin >> a >> b;
             adj[a].push_back(b);
             adj[b].push_back(a);
         }
         cout << installCamera() << endl;
     }

     return ;
 }