P1361 小M的作物 (最大流)

题目

P1361 小M的作物

解析

把\(A\)看做源点，把\(B\)看做汇点，先不考虑额外情况



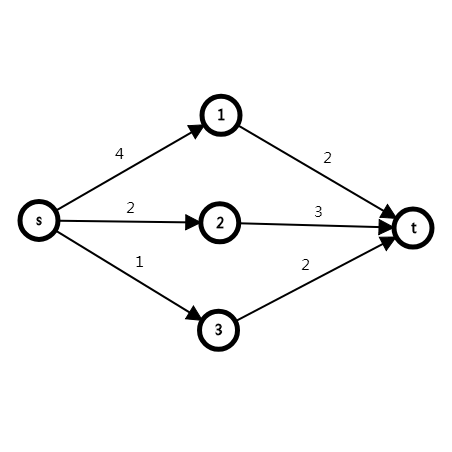
显然，这是一种两者选其一的问题，我们选择一部分边割去，使这部分边的贡献最小，就是求最小割，我们求出了收益最小的情况，又因为只有两种情况，我们取了每一种情况收益较小的一种，所以我们要求的就是总流量-最小割。

然后考虑额外收益的情况，对于每一个额外收益，要么对\(A\)产生影响，要么对\(B\)产生影响，要么两者都不产生影响，所以显然不能直接增加已有的边中的流量，否则会出现同时加\(AB\)的额外贡献的情况，所以建立一个新点，从A向新点连一条边，边权为额外的收益，



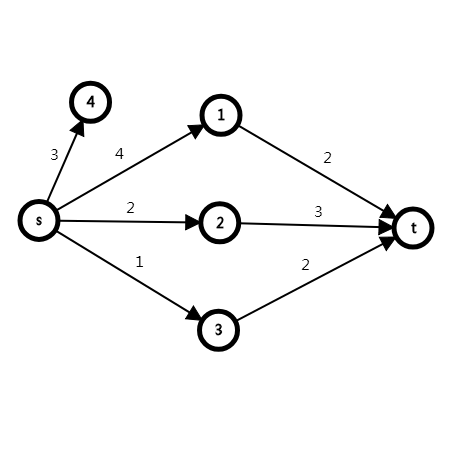
然后从新点向其组合分别连\(INF\)的边，因为如果\(1,2\)被分到了\(B\)田的话，\(s->1,s->2\)的所有路径上都至少要有一条边要断开，我们想要断开\(s->4\)，也就是额外收益的边，怎么办，那就从\(4\)向\(1,2\)连流量为\(INF\)的边，流量为\(INF\)的边不会被切断，注意这里的\(INF\)应为\(0x7fffffff\)。

所以对于\(A\)田这样建图



\(B\)田同理

代码

#include <bits/stdc++.h>
using namespace std;
const int N = 3e6 + 10;
const int INF = 0x7fffffff;
int n, m, num = 1, s, t, sum;
int head[N], cur[N], dep[N];
class node {
	public :
		int v, nx, w;
} e[N];

template<class T>inline void read(T &x) {
	x = 0; int f = 0; char ch = getchar();
	while (!isdigit(ch)) f |= (ch == '-'), ch = getchar();
	while (isdigit(ch)) x = x * 10 + ch - '0', ch = getchar();
	x = f ? -x : x;
	return;
}

inline void add(int u, int v, int w) {
	e[++num].nx = head[u], e[num].v = v, e[num].w = w, head[u] = num;
	e[++num].nx = head[v], e[num].v = u, e[num].w = 0, head[v] = num;
}

queue<int>q;
bool bfs() {
	memset(dep, 0, sizeof dep);
	memcpy(cur, head, sizeof cur);
	dep[s] = 1;
	q.push(s);
	while (!q.empty()) {
		int u = q.front();
		q.pop();
		for (int i = head[u]; ~i; i = e[i].nx) {
			int v = e[i].v;
			if (!dep[v] && e[i].w) dep[v] = dep[u] + 1, q.push(v);
		}
	}
	return dep[t];
}

int dfs(int u, int flow) {
	if (u == t) return flow;
	int use = 0;
	for (int &i = cur[u]; ~i; i = e[i].nx) {
		int v = e[i].v;
		if (e[i].w && dep[v] == dep[u] + 1) {
			int di = dfs(v, min(e[i].w, flow));
			e[i].w -= di, e[i ^ 1].w += di;
			use += di, flow -= di;
			if (flow <= 0) break;
		}
	}
	return use;
} 

int dinic() {
	int ans = 0;
	while (bfs()) ans += dfs(s, INF);
	return ans;
}

int main() {
	memset(head, -1, sizeof head);
	read(n);
	s = 5000, t = s + 1;
	for (int i = 1, x; i <= n; ++i) read(x), add(s, i, x), sum += x;
	for (int i = 1, x; i <= n; ++i) read(x), add(i, t, x), sum += x;
	read(m);
	for (int i = 1, k, a, b; i <= m; ++i) {
		read(k);
		read(a), read(b);
		sum += (a + b);
		add(s, n + i, a), add(n + m + i, t, b);
		for (int j = 1, opt; j <= k; ++j) {
			read(opt);
			add(n + i, opt, INF), add(opt, n + m + i, INF);
		}
	}
	printf("%d\n", sum - dinic());
}