用1 x 2的多米诺骨牌填满M x N矩形的方案数（完美覆盖）

题意

用 $1 \times 2$ 的多米诺骨牌填满 $M \times N$ 的矩形有多少种方案，$M \leq 5,N < 2^{31}$，输出答案模 $p$.

分析

当 $M=3$时，假设前 $n-2$列已经填满，$n-1$ 列不全，现要向左推进一列。

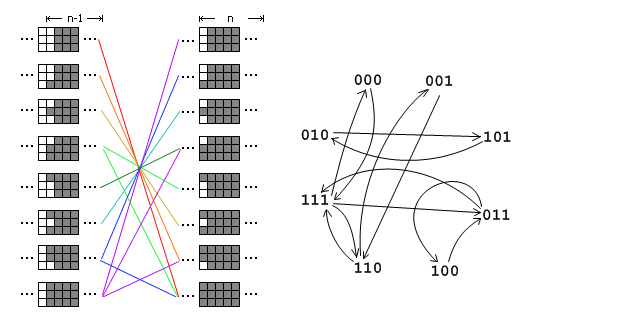
每列只有8种情况，如果一种情况能转移到另一种则连一条边。

答案就是从“111”出发恰好走 $n$ 步又回到“111” 的路径数，这个问题等价于求转移矩阵的 $n$ 次方.

确定转移矩阵，使用矩阵快速幂，$mat[7][7]$ 就是答案。

实现

$M=3$ 时，

#include<cstdio>
#include<cstring>
using namespace std;

typedef long long ll;
struct matrix
{
    int r, c;
    ll mat[][];
    matrix(){
        memset(mat, , sizeof(mat));
    }
};
const ll p = 1e9+;
int n, m=;

matrix mul(matrix A, matrix B)   //矩阵相乘
{
    matrix ret;
    ret.r = A.r; ret.c = B.c;
    for(int i = ;i < A.r;i++)
        for(int k = ;k < A.c;k++)
            for(int j = ;j < B.c;j++)
            {
                ret.mat[i][j] = (ret.mat[i][j] + A.mat[i][k] * B.mat[k][j])%p;
            }
    return ret;
}

matrix mpow(matrix A, int n)
{
    matrix ret;
    ret.r = A.r; ret.c = A.c;
    for(int i = ;i < ret.r;i++)  ret.mat[i][i] = ;
    while(n)
    {
        if(n & )  ret = mul(ret, A);
        A = mul(A, A);
        n >>= ;
    }
    return ret;
}

int  main()
{
    scanf("%d", &n);
    matrix A;
    A.r = A.c = ;
    A.mat[][] = A.mat[][] = A.mat[][] = A.mat[][] = A.mat[][] =
    A.mat[][] = A.mat[][] = A.mat[][] = A.mat[][] = A.mat[][] = A.mat[][] = A.mat[][] = ;
    A = mpow(A, n);
    printf("%lld\n", A.mat[][]);
}

参考链接：

1.http://www.matrix67.com/blog/archives/276

2. https://blog.csdn.net/starcuan/article/details/19076095

3. https://blog.csdn.net/heyuchang666/article/details/68067962