L0、L1与L2范数

监督机器学习问题无非就是“minimize your error while regularizing your parameters”，也就是在正则化参数的同时最小化误差。最小化误差是为了让我们的模型拟合我们的训练数据，而正则化参数是防止我们的模型过分拟合我们的训练数据。

因为参数太多，会导致我们的模型复杂度上升，容易过拟合，也就是我们的训练误差会很小。但训练误差小并不是我们的最终目标，我们的目标是希望模型的测试误差小，也就是能准确的预测新的样本。所以，我们需要保证模型“简单”的基础上最小化训练误差，这样得到的参数才具有好的泛化性能（也就是测试误差也小），而模型“简单”就是通过正则函数来实现的。

一般来说，监督学习可以看做最小化下面的目标函数：

其中，第一项L(y_i,f(x_i;w)) 衡量我们的模型（分类或者回归）对第i个样本的预测值f(x_i;w)和真实的标签y_i之前的误差(loss)。我们不仅要保证训练误差最小，我们更希望我们的模型测试误差小，所以我们需要加上第二项，也就是对参数w的正则函数Ω(w)去约束我们的模型尽量的简单。

对于第一项Loss函数，如果是Square loss，那就是最小二乘(线性回归)了；如果是Hinge Loss，那就是著名的SVM了；如果是exp-Loss，那就是牛逼的 Boosting了；如果是log-Loss，那就是Logistic Regression了

正则项Ω(w)也有很多种选择，一般是模型复杂度的单调递增函数，模型越复杂，正则项值就越大。比如，正则项可以是模型参数向量的范数。

一、L0范数与L1范数

L0范数是指向量中非0的元素的个数。如果我们用L0范数来规则化一个参数矩阵W的话，就是希望W的大部分元素都是0，换句话说，让参数W是稀疏的。

L1范数是指向量中各个元素绝对值之和，也叫“稀疏规则算子”（Lasso regularization）。

为什么L1范数会使权值稀疏？任何的规则化算子，如果他在W_i=0的地方不可微，并且可以分解为一个“求和”的形式，那么这个规则化算子就可以实现稀疏。

既然L0可以实现稀疏，为什么不用L0，而要用L1呢？个人理解一是因为L0范数很难优化求解（NP难问题），二是L1范数是L0范数的最优凸近似，而且它比L0范数要容易优化求解。

让我们的参数稀疏有什么好处呢？这里扯两点：

1）特征选择(Feature Selection)：

大家对稀疏规则化趋之若鹜的一个关键原因在于它能实现特征的自动选择。一般来说，x_i的大部分元素（也就是特征）都是和最终的输出y_i没有关系或者不提供任何信息的，在最小化目标函数的时候考虑x_i这些额外的特征，虽然可以获得更小的训练误差，但在预测新的样本时，这些没用的信息反而会被考虑，从而干扰了对正确y_i的预测。稀疏规则化算子的引入就是为了完成特征自动选择的光荣使命，它会学习地去掉这些没有信息的特征，也就是把这些特征对应的权重置为0。

2）可解释性(Interpretability)：

另一个青睐于稀疏的理由是，模型更容易解释。例如患某种病的概率是y，然后我们收集到的数据x是1000维的，也就是我们需要寻找这1000种因素到底是怎么影响患上这种病的概率的。假设我们这个是个回归模型：y=w₁*x₁+w₂*x₂+…+w₁₀₀₀*x₁₀₀₀+b（当然了，为了让y限定在[0,1]的范围，一般还得加个Logistic函数）。通过学习，如果最后学习到的w*就只有很少的非零元素，例如只有5个非零的w_i，那么我们就有理由相信，这些对应的特征在患病分析上面提供的信息是巨大的，决策性的。也就是说，患不患这种病只和这5个因素有关，那医生就好分析多了。但如果1000个w_i都非0，医生面对这1000种因素，累觉不爱。

二、L2范数

除了L1范数，还有一种更受宠幸的规则化范数是L2范数: ||W||₂。它也不逊于L1范数，它有两个美称，在回归里面，有人把有它的回归叫“岭回归”（Ridge Regression），有人也叫它“权值衰减weight decay”。这用的很多吧，因为它的强大功效是改善机器学习里面一个非常重要的问题：过拟合。至于过拟合是什么，上面也解释了，就是模型训练时候的误差很小，但在测试的时候误差很大，也就是我们的模型复杂到可以拟合到我们的所有训练样本了，但在实际预测新的样本的时候，糟糕的一塌糊涂。

L2范数是指向量各元素的平方和然后求平方根。我们让L2范数的正则项||W||₂最小，可以使得W的每个元素都很小，都接近于0，但与L1范数不同，它不会让它等于0，而是接近于0，这里是有很大的区别的哦。而越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象。为什么越小的参数说明模型越简单？我也不懂，我的理解是：限制了参数很小，实际上就限制了多项式某些分量的影响很小（看上面线性回归的模型的那个拟合的图），这样就相当于减少参数个数。其实我也不太懂，希望大家可以指点下。

实际上，对于L1和L2正则项的损失函数来说，我们可以写成以下形式：

也就是说，我们将模型空间限制在w的一个L1-ball 中。为了便于可视化，我们考虑两维的情况，在(w1, w2)平面上可以画出目标函数的等高线，而约束条件则成为平面上半径为C的一个 norm ball 。等高线与 norm ball 首次相交的地方就是最优解：

可以看到，L1-ball 与L2-ball 的不同就在于L1在和每个坐标轴相交的地方都有“角”出现，而目标函数的测地线除非位置摆得非常好，大部分时候都会在角的地方相交。注意到在角的位置就会产生稀疏性，例如图中的相交点就有w1=0，而更高维的时候（想象一下三维的L1-ball 是什么样的？）除了角点以外，还有很多边的轮廓也是既有很大的概率成为第一次相交的地方，又会产生稀疏性。

相比之下，L2-ball 就没有这样的性质，因为没有角，所以第一次相交的地方出现在具有稀疏性的位置的概率就变得非常小了。这就从直观上来解释了为什么L1-regularization 能产生稀疏性，而L2-regularization 不行的原因了。

因此，一句话总结就是：L1会趋向于产生少量的特征，而其他的特征都是0，而L2会选择更多的特征，这些特征都会接近于0。Lasso在特征选择时候非常有用，而Ridge就只是一种规则化而已。

总结：L1范数和L2范数正则化都有助于降低过拟合风险，但前者还会带来一个额外的好处：它比后者更易于获得稀疏(sparse)解,即它求得的w会有更少的非零分量

---

http://freemind.pluskid.org/machine-learning/sparsity-and-some-basics-of-l1-regularization/

L1产生稀疏性的理解

L1正则：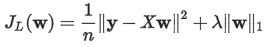

首先,直观上的理解：

上面形式的 LASSO 问题等价于如下形式：

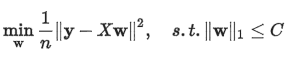
也就是说，我们将模型空间限制在 w 的一个 l1-ball 中。为了便于可视化，我们考虑两维的情况，在$(w_1, w_2)$ 平面上可以画出目标函数的等高线，而约束条件则成为平面上半径为 C 的一个 norm ball 。等高线与 norm ball 首次相交的地方就是最优解。

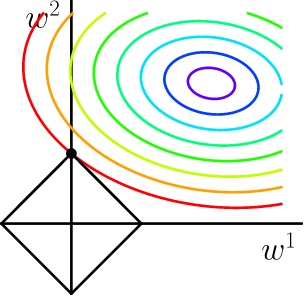
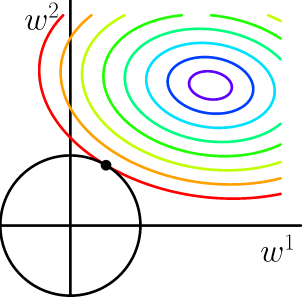
可以看到，l1-ball 与 l2-ball 的不同就在于他在和每个坐标轴相交的地方都有“角”出现，而目标函数的测地线除非位置摆得非常好，大部分时候都会在角的地方相交。注意到在角的位置为产生稀疏性，例如图中的相交点就有$w^1 = 0$  ，而更高维的时候（想象一下三维的 l1-ball 是什么样的？）除了角点以外，还有很多边的轮廓也是既有很大的概率成为第一次相交的地方，又会产生稀疏性。

具体数学上的解释后续再看

http://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html

http://blog.csdn.net/zouxy09/article/details/24972869

https://www.zhihu.com/question/20924039

http://blog.csdn.net/u012162613/article/details/44261657