1 基于梯度的攻击——FGSM

FGSM原论文地址：https://arxiv.org/abs/1412.6572

　　1.FGSM的原理

　　　　FGSM的全称是Fast Gradient Sign Method(快速梯度下降法），在白盒环境下，通过求出模型对输入的导数，然后用符号函数得到其具体的梯度方向，接着乘以一个步长，得到的“扰动”加在原来的输入  上就得到了在FGSM攻击下的样本。

　　　　FGSM的攻击表达如下：

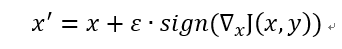
　　　　ε 是一个调节系数，sign() 是一个符号函数，代表的意思也很简单，就是取一个值的符号，当值大于 0 时取 1，当值等于 0 时取 0，当值小于 0 时取 -1，▽ 表示求 x 的梯度，可以理解为偏导，J 是训练模型的损失函数。那么为什么这样做有攻击效果呢？就结果而言，攻击成功就是模型分类错误，就模型而言，就是加了扰动的样本使得模型的loss增大。而所有基于梯度的攻击方法都是基于让loss增大这一点来做的。可以仔细回忆一下，在神经网络的反向传播当中，我们在训练过程时就是沿着梯度方向来更新更新w，b的值。这样做可以使得网络往loss减小的方向收敛。

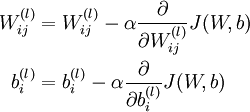
那么现在我们既然是要使得loss增大，而模型的网络系数又固定不变，唯一可以改变的就是输入，因此我们就利用loss对输入求导从而“更新”这个输入。(神经网络在训练的时候是多次更新参数，这个为什么仅仅更新一次呢？主要因为我们希望产生对抗样本的速度更快，毕竟名字里就有“fast”，当然了，多次迭代的攻击也有，后来的PGD（又叫I-FGSM)以及MIM都是更新很多次，虽然攻击的效果很好，但是速度就慢很多了）

　　　　为什么不直接使用导数，而要用符号函数求得其方向？这个问题我也一直半知半解，我觉得应该是如下两个原因：1.FGSM是典型的无穷范数攻击，那么我们在限制扰动程度的时候，只需要使得最大的扰动的绝对值不超过某个阀值即可。而我们对输入的梯度，对于大于阀值的部分我们直接clip到阀值，对于小于阀值的部分，既然对于每个像素扰动方向只有+-两个方向，而现在方向已经定了，那么为什么不让其扰动的程度尽量大呢？因此对于小于阀值的部分我们就直接给其提升到阀值，这样一来，相当于我们给梯度加了一个符号函数了。2.由于FGSM这个求导更新只进行一次，如果直接按值更新的话，可能生成的扰动改变就很小，无法达到攻击的目的，因此我们只需要知道这个扰动大概的方向，至于扰动多少我们就可以自己来设定了~~（欢迎讨论）

　　2.FGSM的进一步解释

　　　　FGSM的原作者在论文中提到，神经网络之所以会受到FGSM的攻击是因为：1.扰动造成的影响在神经网络当中会像滚雪球一样越来越大，对于线性模型越是如此。而目前神经网络中倾向于使用Relu这种类线性的激活函数，使得网络整体趋近于线性。2.输入的维度越大，模型越容易受到攻击。

上图的解释其实也是原论文中的解释，虽然这里是直接使用梯度，没有用符号函数处理过，但道理是一样的。

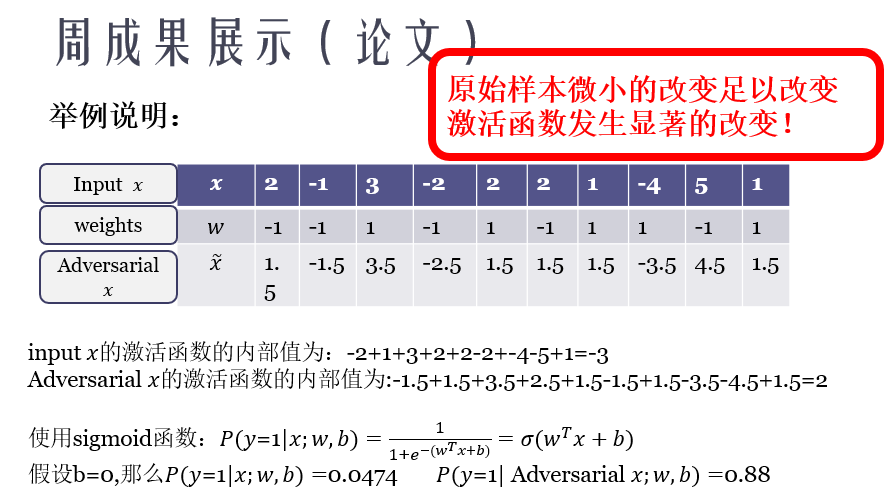
可以看到，对于一个简单的线性分类器，loss对于x的导数取符号函数后即w，即使每个特征仅仅改变0.5，分类器对x的分类结果由以0.9526的置信概率判断为0变成以0.88的置信概率判断为1.　　　

　　3.FGSM的代码实现（pytorch)

 1 class FGSM(nn.Module):
 2     def __init__(self,model):
 3         super().__init__()
 4         self.model=model#必须是pytorch的model
 5         self.device=torch.device("cuda" if (torch.cuda.is_available()) else "cpu")
 6     def generate(self,x,**params):
 7         self.parse_params(**params)
 8         labels=self.y
 9         if self.rand_init:
10             x_new = x + torch.Tensor(np.random.uniform(-self.eps, self.eps, x.shape)).type_as(x).cuda()
11
12         # get the gradient of x
13         x_new=Variable(x_new,requires_grad=True)
14         loss_func = nn.CrossEntropyLoss()
15         preds = self.model(x_new)
16         if self.flag_target:
17             loss = -loss_func(preds, labels)
18         else:
19             loss = loss_func(preds, labels)
20         self.model.zero_grad()
21         loss.backward()
22         grad = x_new.grad.cpu().detach().numpy()
23         # get the pertubation of an iter_eps
24         if self.ord==np.inf:
25             grad =np.sign(grad)
26         else:
27             tmp = grad.reshape(grad.shape[0], -1)
28             norm = 1e-12 + np.linalg.norm(tmp, ord=self.ord, axis=1, keepdims=False).reshape(-1, 1, 1, 1)
29             # 选择更小的扰动
30             grad=grad/norm
31         pertubation = grad*self.eps
32
33         adv_x = x.cpu().detach().numpy() + pertubation
34         adv_x=np.clip(adv_x,self.clip_min,self.clip_max)
35
36         return adv_x
37
38     def parse_params(self,eps=0.3,ord=np.inf,clip_min=0.0,clip_max=1.0,
39                      y=None,rand_init=False,flag_target=False):
40         self.eps=eps
41         self.ord=ord
42         self.clip_min=clip_min
43         self.clip_max=clip_max
44         self.y=y
45         self.rand_init=rand_init
46         self.model.to(self.device)
47         self.flag_target=flag_target

其实FGSM的实现还不是很难~~各个工具包都有实现，可以参考自己实现一下，值得说明的是rand_init和flag_target两个参数：

• 　　rand_init为True时，模型给x求导之前会为其添加一个随机噪声（噪声类型可以自己指定），据说这样效果过会好一点。
• flag_target为False时，即为无目标攻击，此时的loss是loss_func(preds, labels)，这里的lables是正确的lables,当flag_target为False时，即为有目标攻击，此时的loss是-loss_func(preds, labels)，这里的lables是指定的label，故loss前面加负号，这个时候更新x,相当于正常的梯度下降了，因为，这个时候loss_func(preds, labels)是往我们希望的方向优化的。

最后补充一句就是，由于产生的对抗样本可能会在（0，1）这个范围之外，因此需要对x clip至（0，1）。