MT【276】正切的半角公式
若$\Delta ABC$满足:$\tan\dfrac{A}{2}\cdot\tan\dfrac{C}{2}=\dfrac{1}{3},b=\dfrac{4}{3}a$,则$\sin B=$______

分析:$\tan\dfrac{A}{2}\cdot\tan\dfrac{C}{2}=\dfrac{1-\cos A}{\sin A}\cdot\dfrac{\sin C}{1+\cos C}=\dfrac{1}{3}$
得 $\dfrac{a^2-(b-c)^2}{(a+b)^2-c^2}=\dfrac{1}{3}$,得$\dfrac{a-b+c}{a+b+c}=\dfrac{1}{3}$,得$a+c=2b,c=\dfrac{5}{3}a$
故$\angle C=\dfrac{\pi}{2},\sin B =\dfrac{b}{c}=\dfrac{4}{5}$
另附上我两个同事的解答:
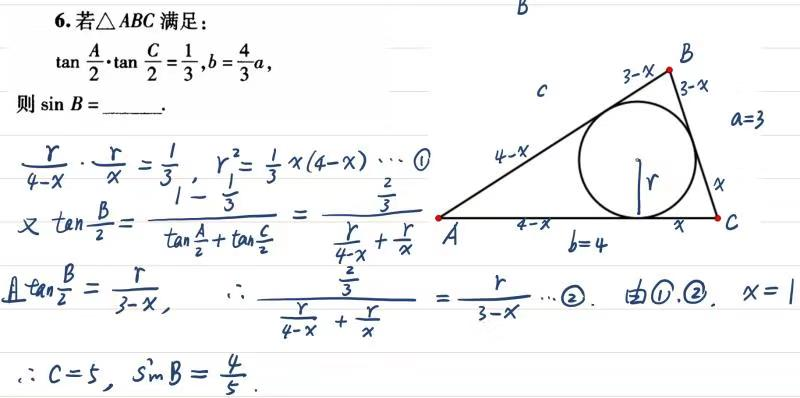
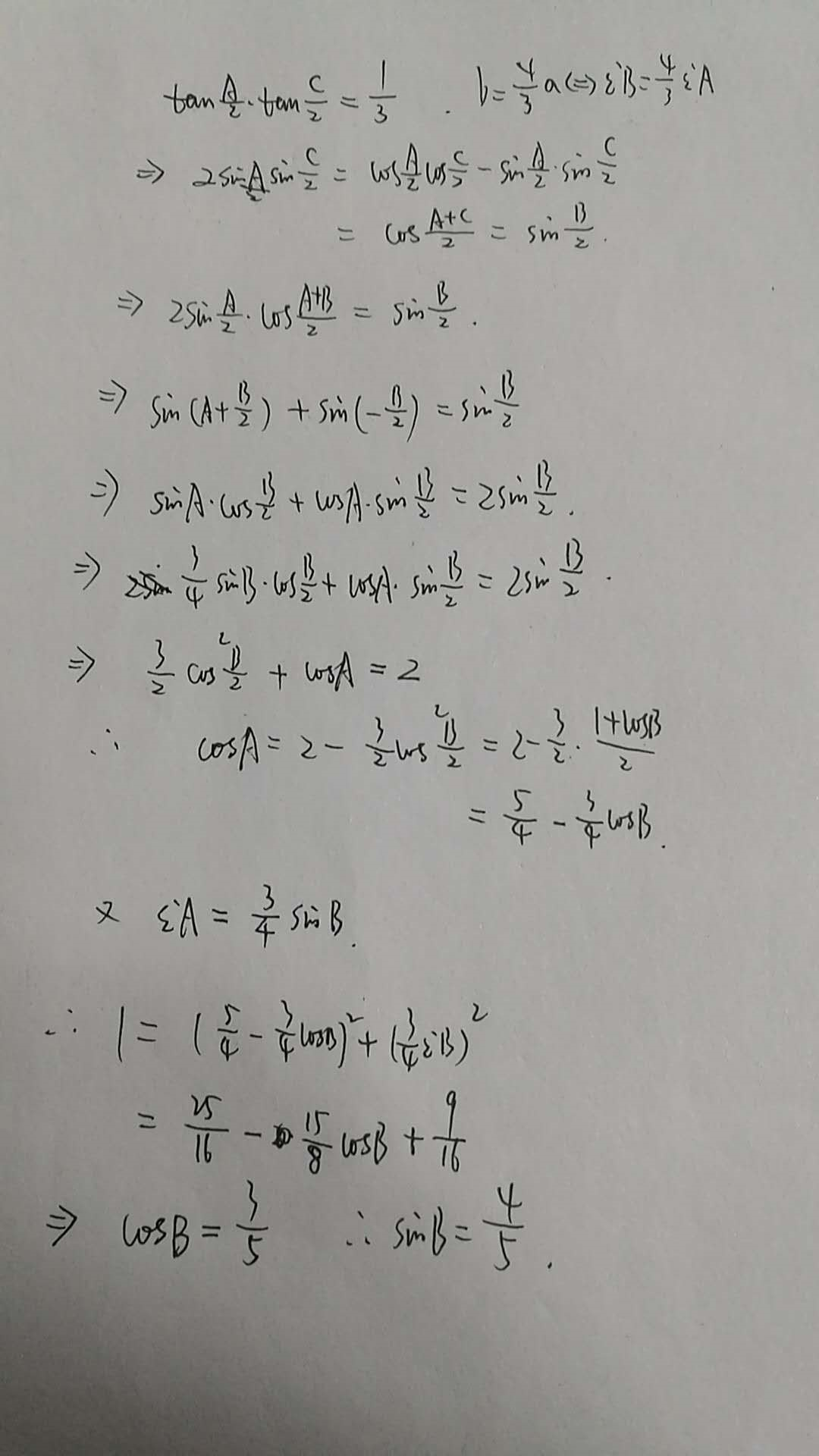
注:$\sum\limits_{cyc}tan\dfrac{A}{2}\tan\dfrac{B}{2}=1$
MT【276】正切的半角公式的更多相关文章
- MT【314】正切比值
(05复旦)已知三角形$\Delta ABC$满足$\tan A:\tan B:\tan C=1:2:3$,求$\dfrac{AC}{AB}$____ 解答:设$x=tan A$,利用恒等式$\tan ...
- MT【188】一个正切余切有关的恒等式
(2017北大特优)求$9\tan 10^\circ+2\tan 20^\circ+4\tan 40^\circ-\tan 80^\circ=$_____ A.$0$ B.$\dfrac{\sqrt ...
- MT【272】更大的视野,更好的思路.
已知$f(x)=\sum\limits_{k=1}^{2017}\dfrac{\cos kx}{\cos^k x},$则$f(\dfrac{\pi}{2018})=$_____ 分析:设$g(x)=\ ...
- 多点触摸(MT)协议(翻译)
参考: http://www.kernel.org/doc/Documentation/input/multi-touch-protocol.txt 转自:http://www.arm9home.ne ...
- /MT、/MD编译选项,以及可能引起在不同堆中申请、释放内存的问题
一.MD(d).MT(d)编译选项的区别 1.编译选项的位置 以VS2005为例,这样子打开: 1) 打开项目的Property Pages对话框 2) 点击左侧C/C ...
- MT写的对URL操作的两个方法
<!doctype html> <html lang="en"> <head> <meta charset="UTF-8&quo ...
- MD(d)、MT(d)编译选项的区别
1.编译选项的位置 以VS2005为例,这样子打开: 1) 打开项目的Property Pages对话框 2) 点击左侧C/C++节 3) 点击Code ...
- DCMTK3.6.0 (MT支持库)安装 完整说明
环境WIN7 + VisualStudio2010 + dcmtk3.6.0 + Cmake2.8.6 准备工作: 从dcmtk官方网站下载源代码及支持库文件.分别名为:dcmtk-3.6.0 dcm ...
- visual studio运行时库MT、MTd、MD、MDd的研究(转载)
转载:http://blog.csdn.net/ybxuwei/article/details/9095067 转载:http://blog.sina.com.cn/s/blog_624485f701 ...
随机推荐
- H5 34-背景图片
<!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8&quo ...
- Python 内置库 sys用法
sys模块功能众多,这边先学习几个常用的方法sys常见函数列表① sys.argv: 实现从程序外部向程序传递参数.其实sys.argv[]就是一个列表,里面的项为用户输入的参数,但是sys.argv ...
- 项目笔记-SC01
项目启动已有两周,从分析需求到系统设计,文档性工作比较多,只是文档参考比较少,相对的标准就不好界定了. 计划开发时间理论上是按部就班的,没什么变化,可能真正进入开发阶段才会遇到一些问题吧,有些问题就是 ...
- Vue之子组件
全局组件 <script src="./static/vue.min.js"></script> // 导入vue <body> <div ...
- 福州大学软件工程1816 | W班 第4次作业(团队展示)成绩排名
作业链接 评分细则 队员姓名与学号(标记组长),其中4-7人一组,特殊情况经老师允许后可以突破限制:(1分) 队名(体现项目内容,并要求有亮点与个性):(1分) 拟作的团队项目描述:一句话(中英文不限 ...
- 多线程系列之三:Immutable 模式
一,什么是Immutable模式?immutable就是不变的,不发生改变的.Immutable模式中存在着确保实例状态不发生变化改变的类.这些实例不需要互斥处理.String就是一个Immutabl ...
- C++实现算法常用的STL---整理
algorithm min(a,b)和max(a,b) #include<iostream> #include<algorithm> using namespace std; ...
- tailf、tail -f、tail -F三者区别(转)
tail -f 等同于--follow=descriptor,根据文件描述符进行追踪,当文件改名或被删除,追踪停止 tail -F 等同于--follow=name --retry,根 ...
- [转帖]PAT 计算机程序设计能力考试
PAT 计算机程序设计能力考试 https://blog.csdn.net/bat67/article/details/52134211 [官方简介] 计算机程序设计能力考试(Programming ...
- C# Note26: [MethodImpl(MethodImplOptions.Synchronized)]与lock机制
在进行.NET开发时,经常会遇见如何保持线程同步的情况.在众多的线程同步的可选方式中,加锁无疑是最为常用的.如果仅仅是基于方法级别的线程同步,使用System.Runtime.CompilerServ ...
