解决重复劳动

是否在分析单个病毒时很爽，分析N个病毒写报告很机械的情况。。

1）样本下载多个文件，这些文件写报告时要加上这些文件的MD5

2）写报告时明明是17个MD5，实际样本有18个的情况。不知道少了的一个MD5到底是谁？

3）要批量检测某一类样本，然后批量复制出来的情况。

后期加入同事的idea，把文件变成hex.txt封印起来。。

命令行版本工具截图

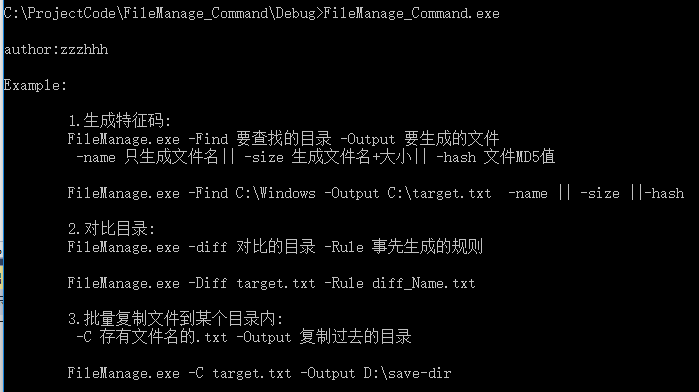
【Windows编程】大量病毒分析报告辅助工具编写的更多相关文章

  1. [FreeBuff]Trojan.Miner.gbq挖矿病毒分析报告

    Trojan.Miner.gbq挖矿病毒分析报告 https://www.freebuf.com/articles/network/196594.html 竟然还有端口转发... 这哥们.. 江民安全 ...

  2. Virut.ce-感染型病毒分析报告

    1.样本概况 病毒名称 Virus.Win32.Virut.ce MD5 6A500B42FC27CC5546079138370C492F 文件大小 131 KB (134,144 字节) 壳信息 无 ...

  3. Windows开发中一些常用的辅助工具

    经常有人问如何快速的定位和解决问题,很多时候答案就是借助工具, 记录个人Windows开发中个人常用的一些辅助工具.   (1) Spy++ 相信windows开发中应该没人不知道这个工具, 我们常用 ...

  4. 一份通过IPC$和lpk.dll感染方式的病毒分析报告

    样本来自52pojie论坛,从事过两年渗透开始学病毒分析后看到IPC$真是再熟悉不过. 1．样本概况 1.1 样本信息 病毒名称:3601.exe MD5值:96043b8dcc7a977b16a28 ...

  5. 爬虫、网页分析解析辅助工具 Xpath-helper

    每一个写爬虫.或者是做网页分析的人,相信都会因为在定位.获取xpath路径上花费大量的时间,甚至有时候当爬虫框架成熟之后,基本上主要的时间都花费在了页面的解析上.在没有这些辅助工具的日子里,我们只能通 ...

  6. 【Android病毒分析报告】 - ZooTiger “集恶意推广、隐私窃取、恶意吸费于一体”

    本文章由Jack_Jia编写,转载请注明出处.  文章链接:http://blog.csdn.net/jiazhijun/article/details/11772379 作者:Jack_Jia    ...

  7. 【Android病毒分析报告】 - ZxtdPay 吸费恶魔

    本文章由Jack_Jia编写,转载请注明出处.  文章链接:http://blog.csdn.net/jiazhijun/article/details/11581543 作者:Jack_Jia    ...

  8. 【Android病毒分析报告】- 手机支付毒王“银行悍匪”的前世今生

    from://http://blog.csdn.net/androidsecurity/article/details/18984165 2014年1月8日,央视曝光了一款名为“银行悍匪”的手机银行木 ...

  9. 2.2 Xpath-helper (chrome插件) 爬虫、网页分析解析辅助工具

    1. Xpath-helper下载 可以直接在chrome浏览器中的扩展程序搜索 Xpath-helper进行添加 也可以直接在http://www.chromein.com/crx_11654.ht ...

随机推荐

  1. 《Linux内核设计与实现》Chapter 2 读书笔记

    <Linux内核设计与实现>Chapter 2 读书笔记 一.获取内核源码 1.使用Git 我们曾经在以前的学习中使用过Git方法 $ git clone git://git.kernel ...

  2. Error:java: 无效的源发行版: 1.8

    出现这种情况是gradle或者maven的版本与 本地电脑jdk不一致,具体看一下链接 http://blog.csdn.net/leixingbang1989/article/details/519 ...

  3. Web网络服务介绍

    Web网络服务也叫WWW(World Wide Web),一般是指能够让用户通过浏览器访问到互联网中文档资源服务.目前提供WEB网络服务的程序有Apache .Nginx 和  IIS  等等,Web ...

  4. Visual Studio(VS)C++单元测试

    版权声明:若无来源注明,Techie亮博客文章均为原创. 转载请以链接形式标明本文标题和地址: 本文标题:Visual Studio(VS)C++单元测试     本文地址:http://techie ...

  5. Python进阶-字符串格式化

    目录 前言 %格式化 str.format() f-Strings 特殊符号处理 前言 在 Python 3.6 之前,字符串格式化方法主要有两种: %格式化 str.format() 在Python ...

  6. ELK环境配置

    一.安装java环境 1.下载jre并安装,安装过程中没有什么特殊的,一直默认下一步即可. 2.配置环境变量 其中变量值为我们安装的jre的路径 二.安装elasticsearch 1.下载es安装包 ...

  7. mysql 命令行快速将数据库转移到另一个服务器中(数据库备份还原)

    想将A服务器中的数据库快速转移到B服务器中,一般是先从A服务器中备份下来,下载备份数据,还原到B服务器中.使用phpMyAdmin备份和还原针对数据量很小的情况下很方便,数据量大的话很容易中断失败. ...

  8. 对象内存空间 在创建对象后 运行时 会把对象的方法放到jvm的方法区中 调用时 将方法拿到栈中 执行完后 这个方法会出栈 然后新的方法方法进栈

  9. BZOJ2442 Usaco2011 Open修剪草坪（动态规划+单调队列）

    显然可以dp.显然可以单调队列优化一下. #include<iostream> #include<cstdio> #include<cmath> #include& ...

  10. hihoCoder 1632 Secret Poems（ACM-ICPC北京赛区2017网络同步赛）

    时间限制:1000ms 单点时限:1000ms 内存限制:256MB 描述 The Yongzheng Emperor (13 December 1678 – 8 October 1735), was ...