python 回溯法 子集树模板 系列 —— 10、m着色问题

问题

图的m-着色判定问题

给定无向连通图G和m种不同的颜色。用这些颜色为图G的各顶点着色，每个顶点着一种颜色，是否有一种着色法使G中任意相邻的2个顶点着不同颜色?

图的m-着色优化问题

若一个图最少需要m种颜色才能使图中任意相邻的2个顶点着不同颜色，则称这个数m为该图的色数。求一个图的最小色数m的问题称为m-着色优化问题。

分析

解的长度是固定的，n。若x为本问题的一个解，则x[i]表示第i个节点的涂色编号。

可以将m种颜色看作每个节点的状态空间。每到一个节点，遍历所有颜色，剪枝，回溯。

不难看出，可以套用回溯法子集树模板。

代码

'''图的m着色问题'''

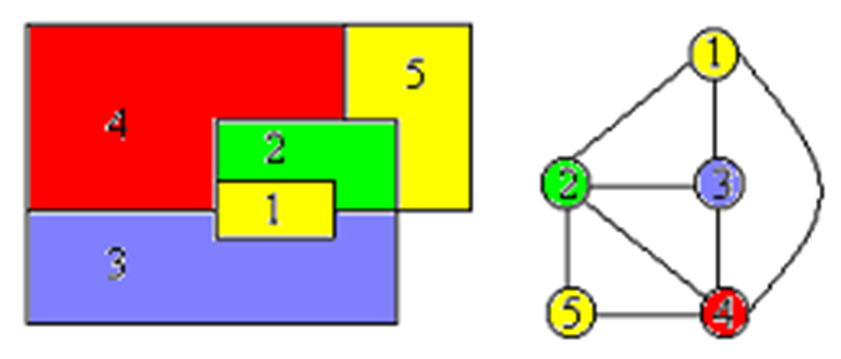
# 用邻接表表示图
n = 5  # 节点数
a,b,c,d,e = range(n) # 节点名称
graph = [
    {b,c,d},
    {a,c,d,e},
    {a,b,d},
    {a,b,c,e},
    {b,d}
]

m = 4  # m种颜色

x = [0]*n  # 一个解（n元数组，长度固定）注意：解x的下标就是a,b,c,d,e!!!
X = []     # 一组解

# 冲突检测
def conflict(k):
    global n,graph,x

    # 找出第k个节点前面已经涂色的邻接节点
    nodes = [node for node in range(k) if node in graph[k]]
    if x[k] in [x[node] for node in nodes]: # 已经有相邻节点涂了这种颜色
        return True

    return False # 无冲突

# 图的m着色（全部解）
def dfs(k): # 到达（解x的）第k个节点
    global n,m,graph,x,X

    if k == n: # 解的长度超出
        print(x)
        #X.append(x[:])
    else:
        for color in range(m): # 遍历节点k的可涂颜色编号（状态空间），全都一样
            x[k] = color
            if not conflict(k): # 剪枝
                dfs(k+1)

# 测试
dfs(a)   # 从节点a开始

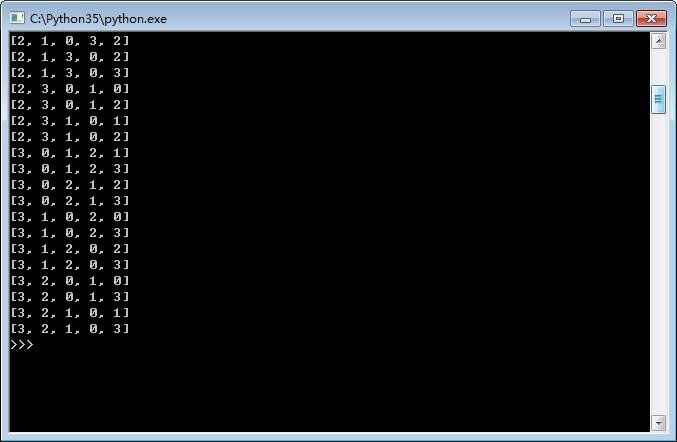
效果图