MATLAB模型预测控制（MPC,Model Predictive Control）

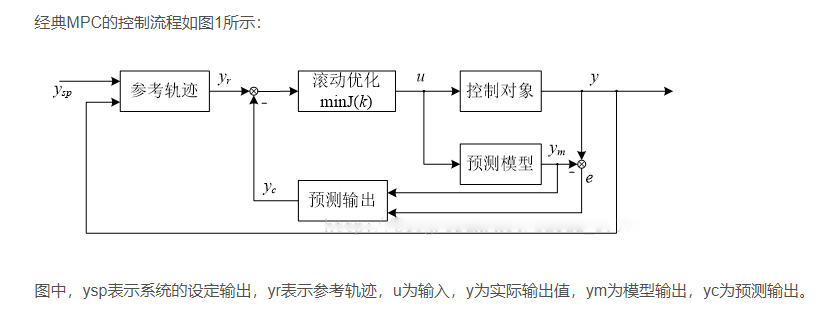
模型预测控制是一种基于模型的闭环优化控制策略。

预测控制算法的三要素：内部（预测）模型、参考轨迹、控制算法。现在一般则更清楚地表述为内部（预测）模型、滚动优化、反馈控制。 
大量的预测控制权威性文献都无一例外地指出, 预测控制最大的吸引力在于它具有显式处理约束的能力, 这种能力来自其基于模型对系统未来动态行为的预测, 通过把约束加到未来的输入、输出或状态变量上, 可以把约束显式表示在一个在线求解的二次规划或非线性规划问题中. 
模型预测控制具有控制效果好、鲁棒性强等优点，可有效地克服过程的不确定性、非线性和并联性，并能方便的处理过程被控变量和操纵变量中的各种约束。

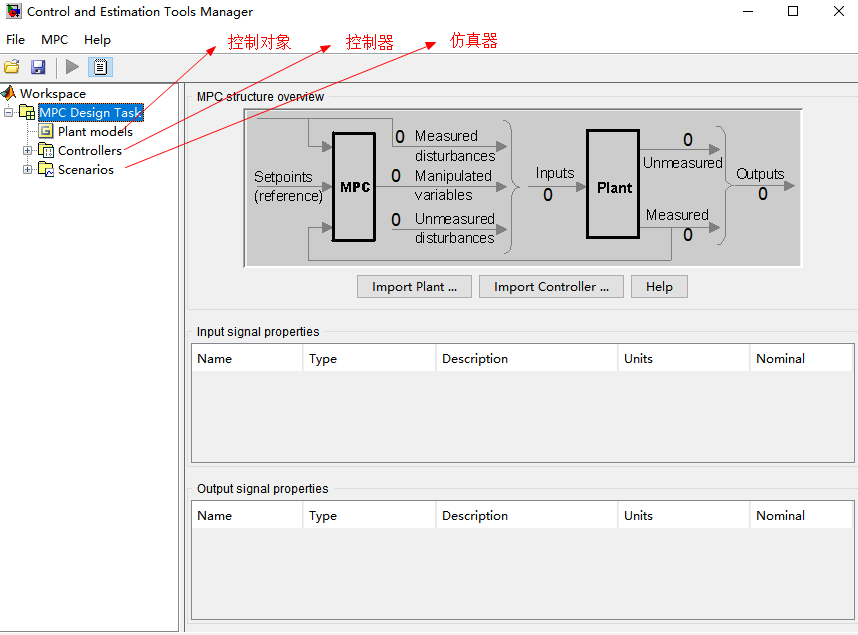
Mo(measured output):当前可测量的输出信号 
Ref(Reference signa):参考信号 
Md(optional measured disturbance signa):可选的测量干扰信号 
Mv（optimal manipulated variables ）：最优操纵变量 
MPC一般通过求解一个二次规划(这里我们使用ord45)来计算最优操纵变量

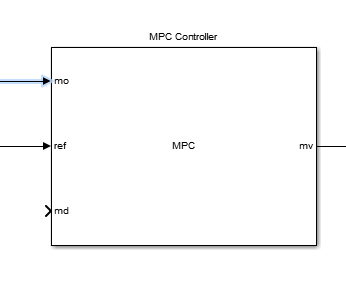
一个简单的例子如下图所示：

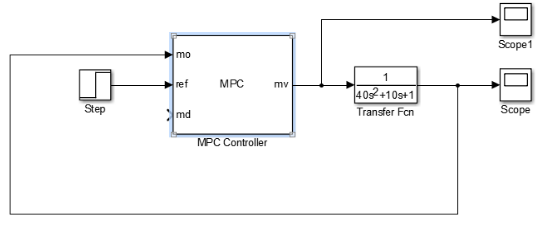
多个MPC调度控制器解决方案

系统描述 ：
如果你的对象模型是非线性,设计一个控制器操作在一个特定的目标地区表现优异，但可能在其他地区表现不佳。补偿的常用方法是设计多个控制器,每个面向一个特定的操作条件的组合。他们之间切换实时随着情况的变化。获得这项技术的调度是一个传统的例子。下面的例子显示了如何协调多个模型预测控制器 
该系统是由两个物体M1和M2分别连接到两个独立的弹簧k1和k2组成。假定当M1和M2碰撞的时候是完全非弹性碰撞。力F对于M1来说是拉力,这是可操纵变量（ manipulated variable MV）。目标是使M1的位置y1跟踪给定参考位置r(Reference signa)。 
当M1和M2分离时,M1自由地移动。发生碰撞的时候,由于是完全非弹性碰撞，所以M1 + M2一起移动。我们假设只有M1的位置和接触传感器提供反馈。后者是用来触发开关MPC控制器来选择MPC1还是MPC2。在这里，我们认为,M2的位置和速度的不可控。在这里，我们认为右方向为正方向

%模型参数%
clear all
clc
M1=;       % M1的质量
M2=;       % M2的质量
k1=;       % 弹簧k1常数k
k2=0.1;     % 弹簧k2常数k
b1=0.3;     % 与空气的摩擦系数，与速度成正比
b2=0.8;     % 摩擦系数
yeq1=;    % 刚性壁1的位置
yeq2=-;   % 刚性壁2的位置

状态空间模型 ：

states：M1的位置和速度 
MV：推力F 
MD：物体１由弹簧的需求的力Ｆ和实际给出的Ｆ之间的常量误差,用来弥补弹簧弹力，使M在初始位置0上时，弹簧对其作用力为零。 
MO：M1的位置

%% 状态空间模型
% 当M1和M2不接触时候的状态模型.
A1=[ ;-k1/M1 -b1/M1];
B1=[ ;-/M1 k1*yeq1/M1];
C1=[ ];
D1=[ ];
sys1=ss(A1,B1,C1,D1);                 %建立状态空间表达式
sys1=setmpcsignals(sys1,'MD',);    %第二个输入是可测量扰动   
%%Setmpcsignals：设置MPC受控对象的的I/0信号模型。这个系统必须是线性时不变系统
%’MD’：可测量的输入扰动，，第二个输入是可测量的输入扰动。如果没有指定的输入变量是MV

结果：

% 当M1和M2接触时候的状态模型.
A2=[ ;-(k1+k2)/(M1+M2) -(b1+b2)/(M1+M2)];
B2=[ ;-/(M1+M2) (k1*yeq1+k2*yeq2)/(M1+M2)];
C2=[ ];
D2=[ ];
sys2=ss(A2,B2,C2,D2);
sys2=setmpcsignals(sys2,'MD',); %第二个输入是可测量扰动   

%%Setmpcsignals：设置MPC受控对象的的I/0信号模型。这个系统必须是线性时不变系统
%’MD’：可测量的输入扰动，，第二个输入是可测量的输入扰动。如果没有指定的输入变量是MV

%%Multi-MPC控制设置
%% MPC仿真参数设置
Ts=0.2;     % 采样时间
p=;       % 预测时域长度
m=;        % 控制时域长度

%% 建立MPC模型
MPC1=mpc(sys1,Ts,p,m);    % 定义M1和M2分离的MPC模型
% 设置限制，F的大小不能为0，F斜率绝对值最大1000
MPC1.MV=struct('Min',,'Max',Inf,'RateMin',-1e3,'RateMax',1e3);

MPC2=mpc(sys2,Ts,p,m);   %定义M1和M2连接的MPC2模型
MPC2.MV=MPC1.MV;          %系统1和系统2的控制限制一样

%% 仿真参数设置
Tstop=;             % 仿真时间
y1initial=;           % 物体1的初始位置
y2initial=;          % 物体2的初始位置
open_system('wc1');   % 调用wc1.MDL
disp('Start simulation by switching control between MPC1 and MPC2 ...');
set_param('wc1/signals','Open','On');%设置系统和模型的参数值
sim('wc1',Tstop);%开始动态系统仿真

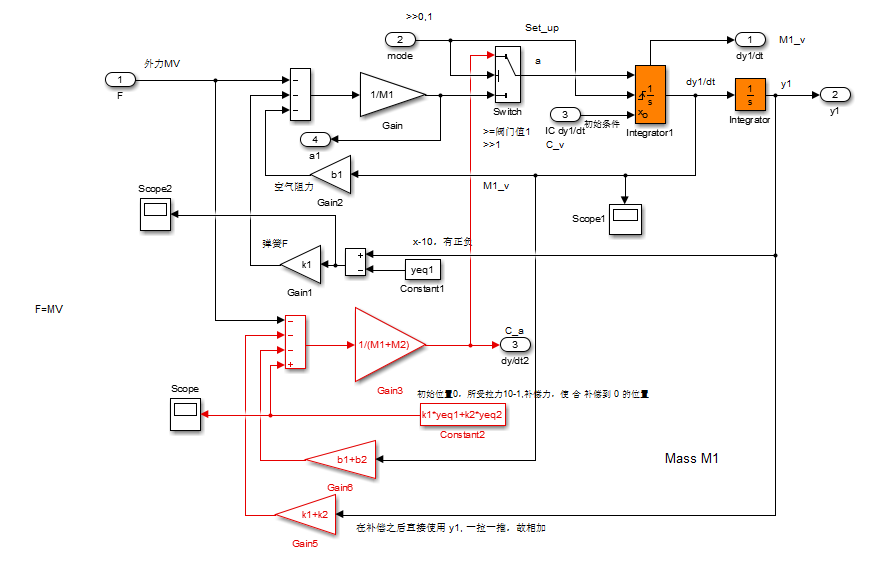
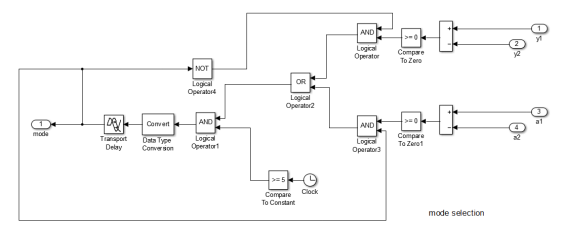
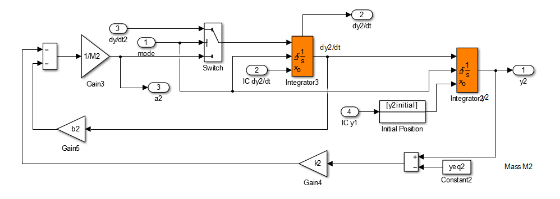
The total simulation diagram上面的部分模拟两个物体的运动，并且这种移动会在在示波器中以信号的方式显示出来。并且当M1的位置和加速度均大于M2的位置和加速度时，model输出布尔量true或者false；下半部分包含以下要素: 
1.多个MPC控制器,。这有四个输入：可测量输出(mo), 参考(ref)，可测量干扰(md)输入和独特的多个MPC控制器的功能块switch输入。 
2.一脉冲发生器改变M1需要到达的位置 (控制器参考信号)。此脉冲发生器的输出是一个幅值为5的方波,频率是0.015每秒。 
3.模拟传感器的接触。当switch输入1时，激活第一个控制器MPC1,这个时候M1和M2是分离的。当两个物体有相同的位置时,Compare to Constant的计算结果为1，通过Add1加法器的输出值为2，Multiple MPC Controllers的switch端口被输入2，自动启动第二个控制器MPC2。

仿真过程展示：

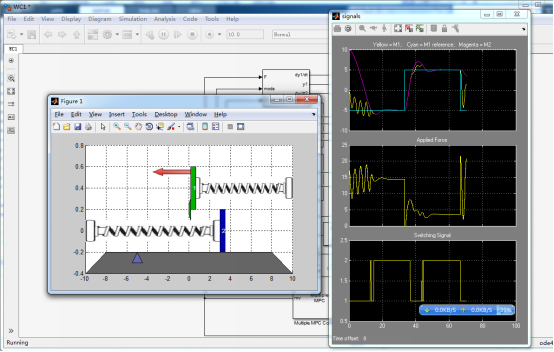
MPC1与MPC2协同工作 
下图展示了对于这个例子多个MPC控制器的仿真：

在图上面上,青色的线（就是我们M1需要的到达的位置，由reference产生）它从-5开始。的M1位置(黄色)从0开始出发。 在MPC1的控制下, M1移动迅速向所需的位置。M2(红色)从10开始开始朝着同一个方向移动 
大约在t = 13秒,M2与M1发生完全非弹性碰撞。M1与M2连在一起。第三幅图显示了开关信号的变化，在这个瞬间从1到2,所以MPC2开始起作用。。 
在M1+M2超过了从其所期望的位置时候，M2和M1仍连在一起。控制器MPC2调整作用力F(中间的图片)使M1+M2快速返回到所需的位置。当r突变到5时，效果一样是非常不错的

%单个MPC1一直工作
%再进行一次无论在什么情况下只用MPC1系统的实验
disp('Now repeat simulation by using only MPC1 ...');
MPC2save=MPC2;     %先将MPC2保存起来
MPC2=MPC1;          %用MPC2来代替MPC21
sim('wc1',Tstop);  %动态系统仿真

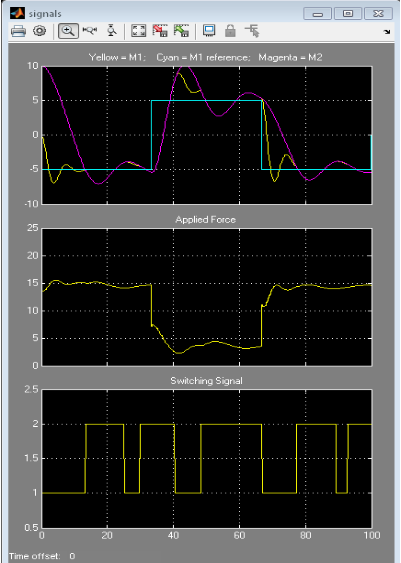
%%如果一直是MPC1的系统，力F不够，当M1和M2链连接在一起的时候，移动缓慢,当下一个转变发生时还不能到达所需的位置

%单个MPC2一直工作
%再进行一次无论在什么情况下只用MPC2系统的实验
disp('Now repeat simulation by using only MPC2 ...');
MPC1=MPC2save;
MPC2=MPC1;
sim('WC1',Tstop);

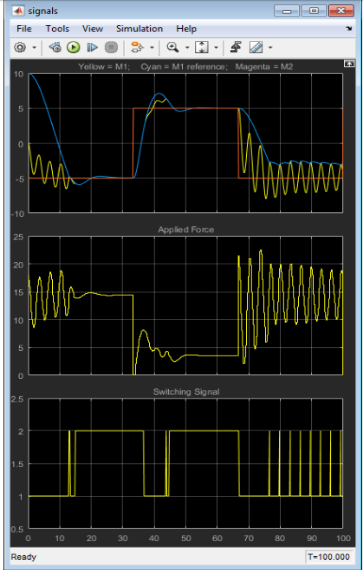
%%当M1和M2分开的时候，MPC2也依然使用，过度使用F，过度补偿,导致振荡产生。当M2和M1连接在一起的时候,移动更平稳,和预期一样。最后过渡造成特别严重的振荡。 M1和M2频繁的碰撞,M1不能到达所需的位置

%%汇总
%% 多个MPC的的调度控制器
% clc
% clear all

%% 系统参数
clear all
clc
M1=;       % M1的质量
M2=;       % M2的质量
k1=;       % 弹簧k1常数k
k2=0.1;     % 弹簧k2常数k
b1=0.3;     % 与空气的摩擦系数，与速度成正比
b2=0.8;     % 摩擦系数
yeq1=;    % 刚性壁1的位置
yeq2=-;   % 刚性壁2的位置   

%% 状态空间模型
% 状态: M的速度和位置
% 被控变量:F
% 可测量的扰动:弹簧1的常熟；
% 测量输出: M1的位置 

% 当M1和M2不接触时候的状态模型.
A1=[ ;-k1/M1 -b1/M1];
B1=[ ;-/M1 k1*yeq1/M1];
C1=[ ];
D1=[ ];
sys1=ss(A1,B1,C1,D1);             %建立状态空间表达式
sys1=setmpcsignals(sys1,'MD',)  ;%第二个输入是可测量扰动

% 当M1和M2接触时候的状态模型.
A2=[ ;-(k1+k2)/(M1+M2) -(b1+b2)/(M1+M2)];
B2=[ ;-/(M1+M2) (k1*yeq1+k2*yeq2)/(M1+M2)];
C2=[ ];
D2=[ ];
sys2=ss(A2,B2,C2,D2);
sys2=setmpcsignals(sys2,'MD',);

%% MPC仿真参数设置
Ts=0.2;     % 采样时间
p=;       % 预测时域长度
m=;        % 控制时域长度

%% 建立MPC模型
MPC1=mpc(sys1,Ts,p,m);                        % 定义M1和M2分离的MPC模型
MPC1.MV=struct('Min',,'Max',Inf,'RateMin',-1e3,'RateMax',1e3);  % 设置限制，F的大小不能为0

MPC2=mpc(sys2,Ts,p,m);       %定义M1和M2连接时候的MPC模型
MPC2.MV=MPC1.MV;             %系统1和系统2的控制限制一样

%% 仿真参数设置
Tstop=;      % 仿真时间
y1initial=;    % 物体1的初始位置
y2initial=;   % 物体2的初始位置
open_system('WC1');   % 调用WC1.MDL

%% 开始三次仿真
%双系统MPC1和MPC2仿真实验
disp('Start simulation by switching control between MPC1 and MPC2 ...');
set_param('wc1/signals','Open','On');%设置系统和模型的参数值
sim('WC1',Tstop);%动态系统仿真

%再进行一次无论在什么情况下只用MPC1系统的实验
disp('Now repeat simulation by using only MPC1 ...');
MPC2save=MPC2;  %先将MPC2保存起来
MPC2=MPC1;      %用MPC2来代替MPC21
sim('WC1',Tstop);

%再进行一次无论在什么情况下只用MPC2系统的实验
disp('Now repeat simulation by using only MPC2 ...');
MPC1=MPC2save;
MPC2=MPC1;
sim('WC1',Tstop);

%% 关闭仿真窗口
% bdclose('WC1')
% close(findobj('Tag','WC1_demo'))

%% reference
%[] A. Bemporad, S. Di Cairano, I. V. Kolmanovsky, and D. Hrovat, "Hybrid
%    modeling and control of a multibody magnetic actuator for automotive
%    applications," in Proc. 46th IEEE(R) Conf. on Decision and Control, New
%    Orleans, LA, .
%[]http://cn.mathworks.com/help/mpc/gs/coordination-of-multiple-model-predictive-controllers.html#bs670e3-8
%[]李国勇，智能预测控制及其MATLAB实现.北京：电子工业出版社，.