poj 2142 The Balance

The Balance

http://poj.org/problem?id=2142

Time Limit: 5000MS		Memory Limit: 65536K

Description

Ms. Iyo Kiffa-Australis has a balance and only two kinds of weights to measure a dose of medicine. For example, to measure 200mg of aspirin using 300mg weights and 700mg weights, she can put one 700mg weight on the side of the medicine and three 300mg weights on the opposite side (Figure 1). Although she could put four 300mg weights on the medicine side and two 700mg weights on the other (Figure 2), she would not choose this solution because it is less convenient to use more weights. 
You are asked to help her by calculating how many weights are required. 

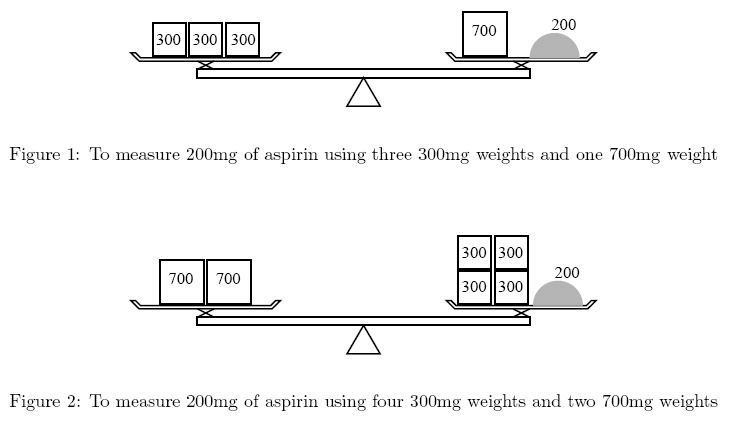
Input

The input is a sequence of datasets. A dataset is a line containing three positive integers a, b, and d separated by a space. The following relations hold: a != b, a <= 10000, b <= 10000, and d <= 50000. You may assume that it is possible to measure d mg using a combination of a mg and b mg weights. In other words, you need not consider "no solution" cases. 
The end of the input is indicated by a line containing three zeros separated by a space. It is not a dataset.

Output

The output should be composed of lines, each corresponding to an input dataset (a, b, d). An output line should contain two nonnegative integers x and y separated by a space. They should satisfy the following three conditions.

• You can measure dmg using x many amg weights and y many bmg weights.
• The total number of weights (x + y) is the smallest among those pairs of nonnegative integers satisfying the previous condition.
• The total mass of weights (ax + by) is the smallest among those pairs of nonnegative integers satisfying the previous two conditions.

No extra characters (e.g. extra spaces) should appear in the output.

Sample Input

700 300 200
500 200 300
500 200 500
275 110 330
275 110 385
648 375 4002
3 1 10000
0 0 0

Sample Output

1 3
1 1
1 0
0 3
1 1
49 74
3333 1

Source

Japan 2004

 

题意：

在天平两侧放若干砝码 和一堆沙子，使天平平衡

即求ax + by = c 的解

若x ，y 为负，表示与沙子放在同一侧，为正表示放在另一侧

题目同时要求 |x|+|y| 最小，在满足其最小的情况下 使 a|x|+b|y|最小

可以先求 使|x|+|y| 最小，在其中找 a|x|+b|y|最小

如何求 |x|+|y|最小？

由 扩展欧几里得算法 可以求出 一组通解（x0，y0）

不熟悉的点这里：http://www.cnblogs.com/TheRoadToTheGold/p/6645383.html

令 d=gcd（a，b）

那么 x= x0 + t*b/d    ，   y=y0 + t*a/d

|x|+|y| = | x0+t*b/d | + | y0-t*a/d |

我们假设 a>b，若输入中a<b，交换

| x0+t*b/d |   单调递增

| y0- t*a/d |   先减后增 

因为 a>b , 所以减的斜率>增的斜率

所以正个函数先减后增

所以 函数必有零点

所以什么时候函数最小？

y0-t*a/d=0时最小

此时 t=y0*d/a

由于取整存在的误差，使函数最小t在t-1到t+1之间

不放心的话 可以扩大范围 t-5到t+5 等等都是没有问题的

#include<cstdio>
#include<algorithm>
using namespace std;
int exgcd(int a,int b,int &x,int &y)
{
    if(!b) {x=; y=; return a;}
    int d=exgcd(b,a%b,x,y);
    int t=x; x=y; y=t-a/b*y;
    return d;
}
int main()
{
    int a,b,c;
    while(scanf("%d%d%d",&a,&b,&c)!=EOF)
    {
        if(!a&&!b&&!c) return ;
        bool f=false;
        if(a<b) swap(a,b),f=true;
        int x,y;
        int d=exgcd(a,b,x,y);
        int x0=c/d*x,y0=c/d*y;
        int t=d*y0/a;
        a/=d; b/=d;
        int add=0x7fffffff,mul=0x7fffffff;
        int ansx,ansy;
        for(int i=t-;i<=t+;i++)
        {
            x=x0+i*b; y=y0-i*a;
            if(x<) x=-x;
            if(y<) y=-y;
            if(x+y<add)
            {
                add=x+y;
                ansx=x;ansy=y;
                mul=a*x+b*y;
            }
            else if(x+y==add)
            {
                if(a*x+b*y<mul)
                {
                    ansx=x;ansy=y;
                    mul=a*x+b*y;
                }
            }
        }
        if(!f) printf("%d %d\n",ansx,ansy);
        else printf("%d %d\n",ansy,ansx);
    }
}