20165203迭代和JDB测试

1.使用C(n,m)=C(n-1,m-1)+C(n-1,m)公式进行递归编程实现求组合数C(m,n)的功能

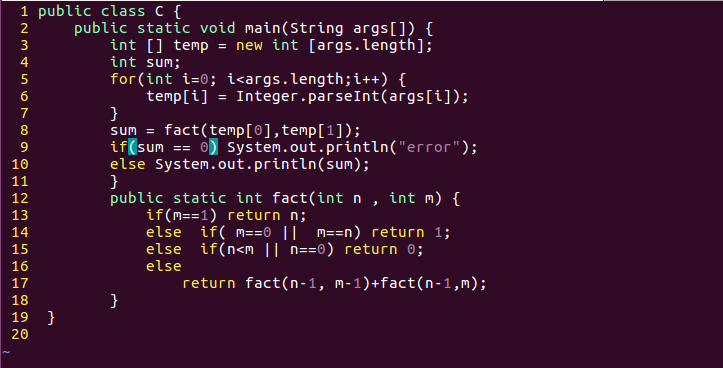
public class C {
    public static void main(String args[]) {
        int [] temp = new int [args.length];
        int sum;
        for(int i=0; i<args.length;i++) {
            temp[i] = Integer.parseInt(args[i]);
        }
        sum = fact(temp[0],temp[1]);
        if(sum == 0) System.out.println("error");
        else System.out.println(sum);
        }
        public static int fact(int n , int m) {
            if(m==1) return n;
            else  if( m==0 ||  m==n) return 1;
            else  if(n<m || n==0) return 0;
            else
                return fact(n-1, m-1)+fact(n-1,m);
        }
 }

2.提交测试运行截图（至少三张：正常如c(3,2)、异常如c(2, 3)、边界情况如c(m,m)）

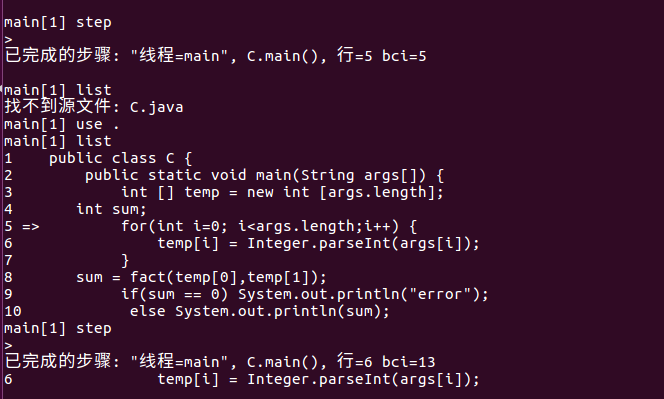
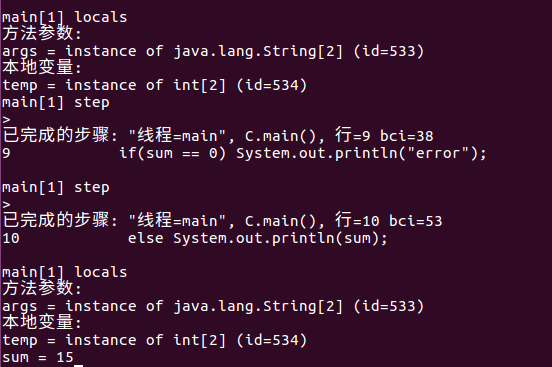
3.提交正常情况下用JDB调试程序c(X,2)的截图,X为学号最后一位+3，至少四张截图