利用for循环如何判定是水仙花数
水仙花数业内的大家可能听说过,但是对于初学者来讲,对于水仙花数还是比较陌生的。
首先要知道的是水仙花数的计算公式:153=1**3+5**3+3**3:
如何去判定这个数是否为水仙花数,最好的办法就是用for内嵌循环了,因为涉及到了公式所以很多数学逻辑不是很好的兄台,就尴尬了,其实有一个比较简单的数学逻辑来运算,如设定一个1-999的水仙花数, 程序如下:
for x in range(1,10): #百位数的计算
for y in range(1,10):#十位数的计算
for z in range(1,10):#个位数的计算
i=x*100+y*10+z*1
if x**3+y**3+z**3==i:
print(i)
那么这段代码首先是区分开来首先算出个百位,十位,个位的数,在进行下一步的判定。
举例说明:
for x in range(1,10): #外循环第一层循环 x=1
for y in range(1,10)# #内循环环第二层循环 y=1
for z in range(1,10): #第三层循环第一层循环 z=1
那么现在这个结构就是 x=1,y=1 z =1,这个三个数字分别的站位不同 x是百位,y的十位z是个位,但是我们要求是100-999的数所以下一步我们要这么做,将xyz这三个值根据站位来相乘并相加x*100+y10+z*1那么现在三个(xyz)循环是111,一个变量,方便下面的程序调用。i=x*100+y*10+z*1
我们要给这段表达式设置刚开始我们说了水仙花数的计算公式是每个值的三次方,下面我们就可以直接判定:
if x**3+y**3+z**3==i:
如果x的3次方加上y的3次方再加上z的三次方等于我们设置的变量i的话那么他就是水仙花数!
执行结果如下:
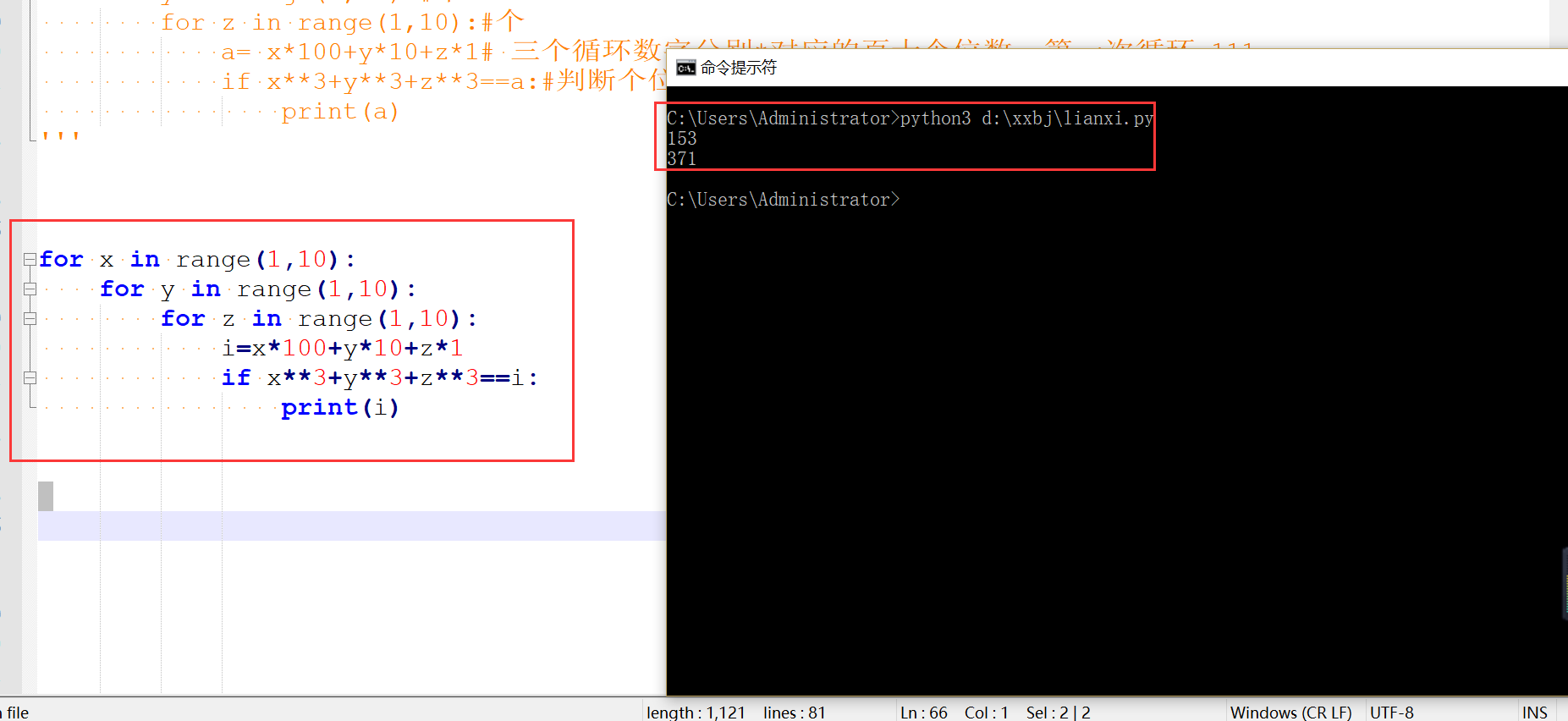
利用for循环如何判定是水仙花数的更多相关文章
- for循环与嵌套(水仙花数与三角形的打印)
## 一.for循环语法:for(开始区间: 结束区间; 修改循环条件){ 循环体:} > 开始区间:初始化表达式(确定开始)int i = 1; > 结束区间:逻辑表达式(确定结束) i ...
- 求n位水仙花数
求n位水仙花数 A.两个关键 1.n位水仙花数的范围是什么? n位水仙花数的范围是[10n-1,10n) 2.如何判断是否为水仙花数 核心操作: 2-1.如何得到每一位? A.核心思想 对得到的数进行 ...
- Tips_of_JS 之 利用JS实现水仙花数的寻找与实现斐波那契数列
一.水仙花数 1.啥是水仙花数? 水仙花数是指一个 n 位正整数 ( n≥3 ),它的每个位上的数字的 n 次幂之和等于它本身.(例如:1^3 + 5^3+ 3^3 = 153) 2.利用JS实现对水 ...
- 【Java基础】for循环实现在控制台打印水仙花数
代码: /* * 需求:在控制台输出所有的”水仙花数” * * 分析: * 什么是水仙花数呢? * 所谓的水仙花数是指一个三位数,其各位数字的立方和等于该数本身. * 举例:153就是一个水仙花数. ...
- 用js 的for循环打印三角形,提取水仙花数,求本月多少天
第一题:用for循环打印三角形 //第一个 for(var x = 1;x <= 4;x++){ //控制行数 :由 1 到 4 for(var y = 1;y <= x;y++){ // ...
- 【C语言】(for循环嵌套)找出1000以内的水仙花数
什么是水仙花数? 水仙花数是指一个 3 位数,它的每个位上的数字的 3次幂之和等于它本身(例如:1^3 + 5^3+ 3^3 = 153). 分析: 根据定义可知: a*a*a+b*b*b+c*c*c ...
- 水仙花数的条件:1.是一个三位数,2.个百千位数字的3次方加起来的和等于当前的三位数。如果,想要完美一点可以在外部加while循环
#!/usr/bin/env python# -*- coding: utf-8 -*-print("请输入三位数:")num = input()# 定义常量SumNum = 0# ...
- 初入PHP,(for循环~水仙花数)
找出100-999之间的所有"水仙花数".所谓水仙花数是指一个三位 数,各位数字的立方和等于该数本身.(如153次方=1的3次方+5的3次方+3的3次方)并输出这些数字 想想153 ...
- 练习十三:水仙花数,用for循环实现
水仙花数是指一个n位正整数(n>=3),他得每个位上得数字得n次幂之和等于它本身(例如:1^3+5^3+3^3=153) for i in range(101,1000): #3位数得水仙花数 ...
随机推荐
- [T-ARA][Bye Bye]
歌词来源:http://music.163.com/#/song?id=22704472 사랑하는 그대 Bye Bye, Bye Bye, Bye Bye, [sa-lang-ha-neun geu ...
- 【原创】python __all__ 的用法
1. 写自己的module或者package的时候需要控制向外暴露的名字, 这个很有用, 防止名字污染
- JNI学习笔记
JNI是什么->一套c和java的互掉规则 为什么使用JNI 1.非常多敏感效率的代码已经用C实现了 2. JNI双向.java调用c,c调用java Java集成本地代码问题 1.代码 ...
- linux用户相关及/etc/passed,/etc/group,/etc/shadow
useradd:新建用户 usermod:修改用户相关信息 userdel:删除用户分(-r选项) 组的操作与用户的操作类似 选项 userdel相关选项: -f:强制删除用户,即使用户已登录 -r: ...
- Ansible--01
一.ansible是什么: 类似puppet之类的运维自动化工具 二.为什么选择ansible: 1. ansible是python语言开发的,python语言进入门槛低,方便基于pytnon对ans ...
- oracle ORA-01722:无效数字 记录
今天在对12万条记录的表进行左联接时,有时可以查询出数据,有时会报无效数字,反复检查,发现问题. 例如sql: SELECT * FROM USER U LEFT JOIN USER_ROLE UR ...
- 学习笔记——并行编程Parallel
Parallel 并行运算 参考资料:http://www.cnblogs.com/woxpp/p/3925094.html 1.并行运算 使用Parallel并行运算时,跟task很像,相当于tas ...
- UML基础—结构和组成
本文主要梳理了一下UML2中的各个图的逻辑划分,UML基础知识. 一.UML2的4个规范 二.UML2的13种模型图 分为3大类:行为视图.交互视图.结构视图 三.UML1和UML2各种视图对照 四. ...
- Linux 和 ubuntu安装redis
Linux 下安装reids 下载地址:http://redis.io/download,下载最新稳定版本. 本教程使用的最新文档版本为 2.8.17,下载并安装: $ wget http://dow ...
- 克隆虚拟机及配置yum源的步骤及讲解(Hadoop基础)
1.克隆虚拟机 找一台需要克隆的虚拟机但虚拟机必须在关机下进行,(建议将前期Linux环境 配置完成) 在VMware中右键虚拟机找到克隆的选项. 点击克隆 可以克隆他的快照(提前做快照)或者是克 ...
