poj 2451 Uyuw's Concert（半平面交）

Uyuw's Concert

Time Limit: 6000MS		Memory Limit: 65536K
Total Submissions: 8580		Accepted: 3227

Description

Prince Remmarguts solved the CHESS puzzle successfully. As an award, Uyuw planned to hold a concert in a huge piazza named after its great designer Ihsnayish.

The piazza in UDF - United Delta of Freedom’s downtown was a square
of [0, 10000] * [0, 10000]. Some basket chairs had been standing there
for years, but in a terrible mess. Look at the following graph.



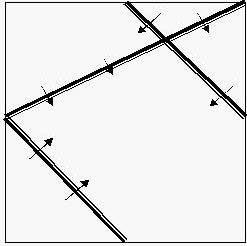
In this case we have three chairs, and the audiences face the
direction as what arrows have pointed out. The chairs were old-aged and
too heavy to be moved. Princess Remmarguts told the piazza's current
owner Mr. UW, to build a large stage inside it. The stage must be as
large as possible, but he should also make sure the audience in every
position of every chair would be able to see the stage without turning
aside (that means the stage is in the forward direction of their own).

To make it simple, the stage could be set highly enough to make sure
even thousands of chairs were in front of you, as long as you were
facing the stage, you would be able to see the singer / pianist – Uyuw.

Being a mad idolater, can you tell them the maximal size of the stage?

Input

In
the first line, there's a single non-negative integer N (N <=
20000), denoting the number of basket chairs. Each of the following
lines contains four floating numbers x1, y1, x2, y2, which means there’s
a basket chair on the line segment of (x1, y1) – (x2, y2), and facing
to its LEFT (That a point (x, y) is at the LEFT side of this segment
means that (x – x1) * (y – y2) – (x – x2) * (y – y1) >= 0).

Output

Output a single floating number, rounded to 1 digit after the decimal point. This is the maximal area of the stage.

Sample Input

3
10000 10000 0 5000
10000 5000 5000 10000
0 5000 5000 0

Sample Output

54166666.7

Hint

Sample input is the same as the graph above, while the correct solution for it is as below:


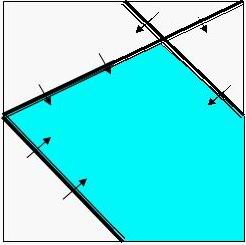
I suggest that you use Extended in pascal and long double in C / C++
to avoid precision error. But the standard program only uses double.

Source

POJ Monthly,Zeyuan Zhu

【思路】

半平面交。

注意设置边界，输入向量方向和eps选择，1e-10足够。

【代码】

 #include<cmath>
 #include<cstdio>
 #include<vector>
 #include<cstring>
 #include<algorithm>
 #define FOR(a,b,c) for(int a=(b);a<=(c);a++)
 using namespace std;

 const int eps = 1e-;

 struct Pt {
     double x,y;
     Pt (double x=,double y=) :x(x),y(y) {}
 };
 typedef Pt vec;

 vec operator - (Pt a,Pt b) { return vec(a.x-b.x,a.y-b.y); }
 vec operator + (vec a,vec b) { return vec(a.x+b.x,a.y+b.y); }
 vec operator * (vec a,double x) { return vec(a.x*x,a.y*x); }

 double cross(Pt a,Pt b) { return a.x*b.y-a.y*b.x; }

 struct Line {
     Pt p; vec v; double ang;
     Line() {}
     Line(Pt p,vec v) :p(p),v(v) { ang=atan2(v.y,v.x); }
     bool operator < (const Line& rhs) const {
         return ang < rhs.ang;
     }
 };
 //p在l的左边
 bool onleft(Line L,Pt p) { return cross(L.v,p-L.p)>; }
 Pt getLineInter(Line a,Line b) {
     vec u=a.p-b.p;
     double t=cross(b.v,u)/cross(a.v,b.v);
     return a.p+a.v*t;
 }

 vector<Pt> HPI(vector<Line> L) {
     int n=L.size();
     sort(L.begin(),L.end());
     int f,r;
     vector<Pt> p(n) , ans;
     vector<Line> q(n);
     q[f=r=]=L[];
     for(int i=;i<n;i++) {
         while(f<r && !onleft(L[i],p[r-])) r--;
         while(f<r && !onleft(L[i],p[f])) f++;
         q[++r]=L[i];
         if(fabs(cross(q[r].v,q[r-].v))<eps) {
             r--;
             if(onleft(q[r],L[i].p)) q[r]=L[i];
         }
         if(f<r) p[r-]=getLineInter(q[r-],q[r]);
     }
     while(f<r && !onleft(q[f],p[r-])) r--;
     if(r-f<=) return ans;
     p[r]=getLineInter(q[r],q[f]);
     for(int i=f;i<=r;i++) ans.push_back(p[i]);
     return ans;
 }
 vector<Line> L;
 vector<Pt> p;
 int n;

 int main() {
     //freopen("in.in","r",stdin);
     //freopen("out.out","w",stdout);
     scanf("%d",&n);
     double x1,y1,x2,y2;
     for(int i=;i<n;i++) {
         scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
         Pt a(x1,y1) , b(x2,y2);
         L.push_back(Line(a,b-a));
     }
     Pt a(,),b(,),c(,),d(,);
     L.push_back(Line(a,b-a));
     L.push_back(Line(b,c-b));
     L.push_back(Line(c,d-c));
     L.push_back(Line(d,a-d));
     p = HPI(L);
     double ans=; int m=p.size();
     for(int i=;i<m-;i++)
         ans += cross(p[i]-p[],p[i+]-p[]);
     printf("%.1lf",ans/);
     return ;
 }