[luogu1447][bzoj2005][NOI2010]能量采集

题目大意

求出\(\sum_{i=1}^{n} \sum_{i=1}^{m} gcd(i,j)\times 2 -1\)。

题解

解法还是非常的巧妙的，我们考虑容斥原理。我们定义\(f[i]\)表示\(gcd(x,y)\)的数对的个数，但是我们可以发现这样的状态并不好直接转移。那么我们就从\(f[i]\)的倍数入手（也就是\(gcd(x,y)\)的倍数入手，这样比较好理解），先定义\(g[i]\)为在数对\((x,y)\)中\(gcd(x,y)\)是\(i\)的倍数的个数。这种思想比较像线性筛素数。

对于一开始的\(g[i]\)就是\(\frac{n\times m}{i^2}\)。关于这个玩意的证明我还是不怎么会，但是好像听其他大佬说：你太弱了，这是显而易见的。（emm~~我果然是太弱了）

那么我们就当这个东西是显而易见的好了，如果有证明我会回来补坑的。（应该也有很多小伙伴也不知道这个东西怎么证明）（可能是我太菜了，不要吐槽我QAQ）。

---

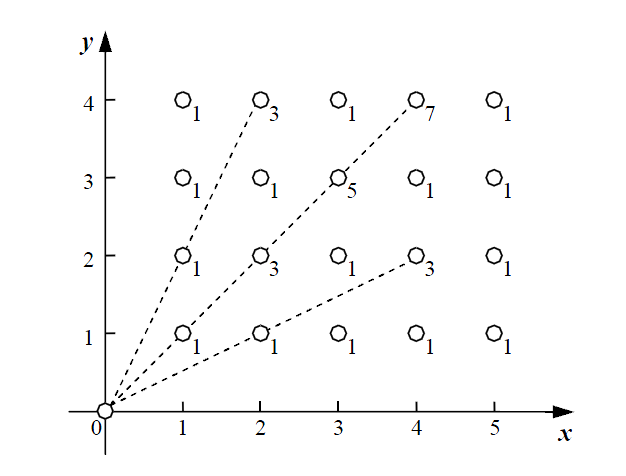
证明（update by 2019/3/3 19.33）

是我脑子出问题了，其实画一个图就出来的事情，还搞得怎么复杂。证明简单，如下：
已知：\(x\in [1,n]\)且\(y\in [1,m]\)。
求证：\(gcd(x,y)\)的倍数（包括\(1\)倍）的个数有\(\frac{n\times m}{gcd(x,y)^2}\)。
证明：我们假设\(g=gcd(x,y)\)，那么可以得到最小的数对就是\((1,g)\)和\((g,1)\)，那么非常显然数对\((g,g)\)的\(gcd\)也是\(g\)的倍数，那么也可以推出在\([1,n]\)和\([1,m]\)的范围内，在横排上有\(n/g\)和\(m/g\)，根据乘法原理，所有的点对的个数就是\(n*m/(g^2)\)。

---

得到这些倍数之后，因为我们是算倍数，在\(g[i]\)中包含了\(g[i\times 2]+\cdots+g[i\times k] \ (i\times k<=min(n,m))\)，那么容斥原理把这些重复的部分减去就可以了，也就是\(f[i]=f[i]-g[i\times2]-g[i\times3]-\cdots-g[i\times k] \ (i\times k<=min(n,m))\)

小小的细节：因为我们是要算出倍数，那么我们倍数必须要先算出来，那么在枚举是我们要从后向前枚举，是不是非常好理解。

ac代码

# include <cstdio>
# include <cstring>
# include <algorithm>
# include <ctype.h>
# include <iostream>
# include <cmath>
# include <map>
# include <vector>
# include <queue>
# define LL long long
# define ms(a,b) memset(a,b,sizeof(a))
# define ri (register int)
# define inf (0x7f7f7f7f)
# define pb push_back
# define fi first
# define se second
# define pii pair<int,int>
# define File(s) freopen(s".in","r",stdin),freopen(s".out","w",stdout)
using namespace std;
inline int gi(){
    int w=0,x=0;char ch=0;
    while(!isdigit(ch)) w|=ch=='-',ch=getchar();
    while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
    return w?-x:x;
}
# define N 100005
int n,m;
LL ans,f[N];
int main(){
    n=gi(),m=gi();
    for (int i=n;i>=1;i--){
        f[i]=(LL)(n/i)*(m/i);
        for (int j=2*i;j<=min(n,m);j+=i) f[i]-=f[j];//容斥原理，减去重复的部分
        ans+=(LL)(i*2-1)*f[i];
    }
    printf("%lld\n",ans);
    return 0;
}