吴恩达机器学习CS229课程笔记学习

监督学习（supervised learning）

假设我们有一个数据集（dataset），给出居住面积和房价的关系如下：

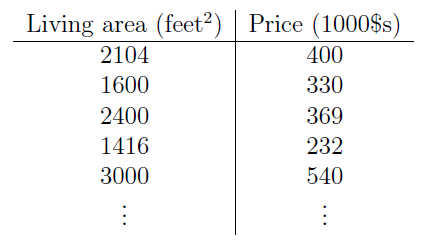
我们以居住面积为横坐标，房价为纵坐标，组成数据点，如（2104, 400），并把这些数据点描到坐标系中，如下：

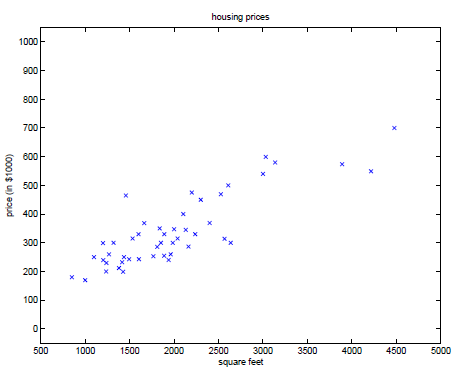
由这些数据，我们怎么才能预测（predict）其他房价呢？其中房价作为居住面积的函数。

为了方便描述，我们用x⁽ⁱ⁾表示输入变量（即居住面积），也叫做输入特征（features）；同时，用y⁽ⁱ⁾表示输出（即房价），也叫做目标（target）变量。有序对   (x⁽ⁱ⁾, y⁽ⁱ⁾)叫做一个训练样本点（training example）；我们用来学习（learn）的数据集，包含m个样本点，也叫做训练集（training set），表示为{(x⁽ⁱ⁾, y⁽ⁱ⁾); i=1,...,m}。其中上标(i)表示样本点在训练集中的索引，跟指数没关系。另外，我们用X表示输入变量的取值空间，Y表示输出的取值空间，在本文中，X=Y=R。

我们的目的就是学习出一个函数h: X->Y，使得h(x)能够很好的预测y，即|h(x)-y|越小越好。由于历史原因，函数h也叫做假设（hypothesis）。整个流程形象化描述下：

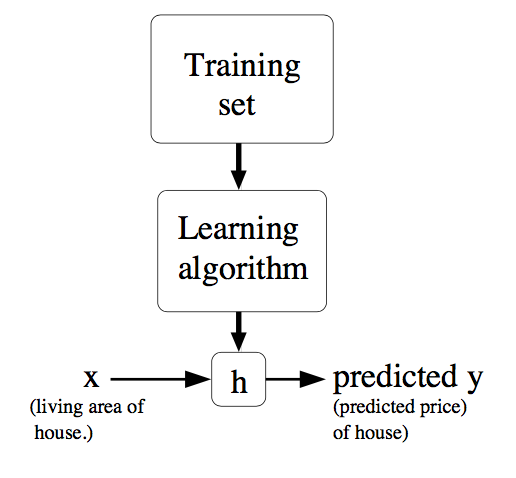
当我们想要预测的目标变量是连续的（continuous），这种学习问题被称之为回归（regression）；而离散（discrete）时，则叫做分类（classification）。

线性回归（linear regression）

为了让上面的问题更加一般化，假设我们除了居住面积和房价，还知道房间个数，如下：

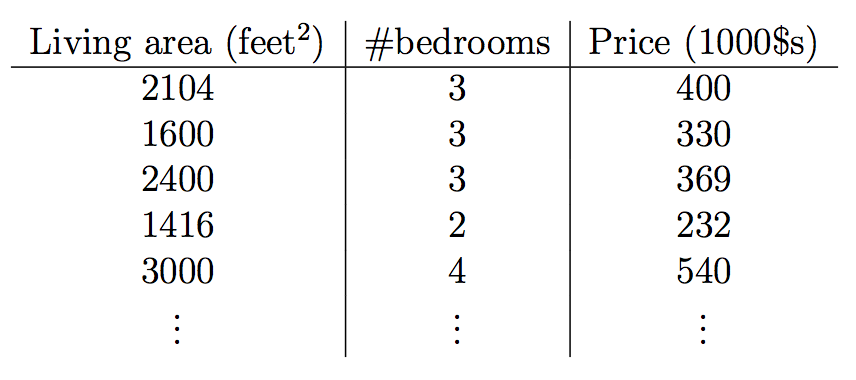
这样，x就是2维空间R²中的向量。x₁⁽ⁱ⁾表示训练集中第i个房子的居住面积，而x₂⁽ⁱ⁾就是它的房间个数。

学习之前，我们需要先决定函数h的表达式。最原始的想法就是，用x的线性函数来拟合（approximate）y。如下：

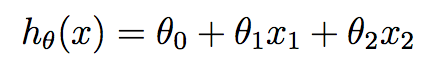
其中，θ_i 是参数，也叫权值（weight）。在不会引起误解的情况下，我们通常把h_θ(x)中的下标θ去掉，简单表示为h(x)。进一步地，我们令x₀=1（即截距），使得：

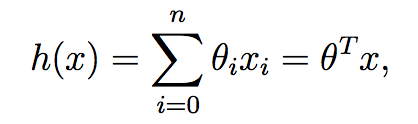
上式中，我们把θ和x都看做向量，这里其实是行向量，θ^T是θ的转置（即对应的列向量）。这里之所以要转成列向量，是因为要把两个向量的数量积看做是两个矩阵相乘。

有了函数表达式，接下来就是要利用训练集把参数θ学习出来。为此，我们定义代价函数（cost function）如下：

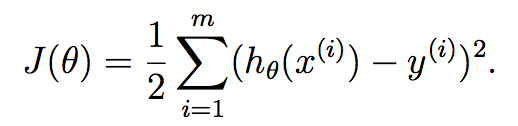
为什么这样定义代价函数呢？如果以前看过最小二乘法（least-squres），就会很熟悉上式。

LMS（Least Mean Square，最小均方）算法

我们需要找出使得代价J(θ)最小的θ。为此，我们估算一个θ的初始值，并不断改变它使得J(θ)更小，直到J(θ)不能再小。具体做法是利用梯度下降（gradient descent）算法，给θ赋一个初始值，然后按照如下表达式不断更新：

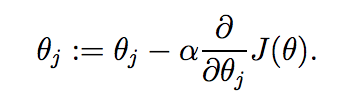
上式更新对θ向量的每个分量θ_j(j=0,...,n)是同时进行的，其中α叫做学习率（learning rate）。 接下来，我们需要解出右边的偏导（partial derivative），不失一般性地，先假设训练集中只有一个样本（x, y），这样，我们就可以忽略J(θ)中的累加运算，得到如下计算过程，这里需要熟悉导数运算法则，另外，求导的关键在于，对谁求导，谁就是变量，其他都是常量：

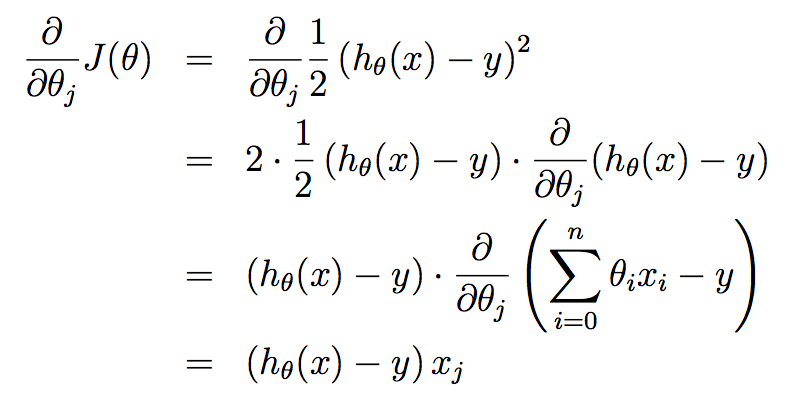
把计算后的偏导代回原式，就可以得到如下更新规则（即LMS更新规则），也叫Widrow-Hoff学习规则：

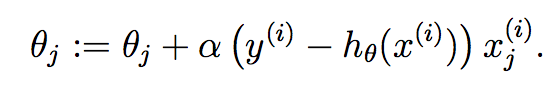
从上式更新规则可以看出，θ_j的更新增量α(y⁽ⁱ⁾-h_θ(x⁽ⁱ⁾))x_j⁽ⁱ⁾跟y⁽ⁱ⁾-h_θ(x⁽ⁱ⁾)成正比。通俗来讲就是，当预测值h_θ(x⁽ⁱ⁾)接近真实值y⁽ⁱ⁾，即误差（error）越小时，参数θ_j需要做出的更新越小，反之同理。上述更新规则是通过一个样本计算出来的，推广到m个样本呢？有两种方法，第一种就是把之前的累加运算补回来（因为和的导数等于导数的和），如下：

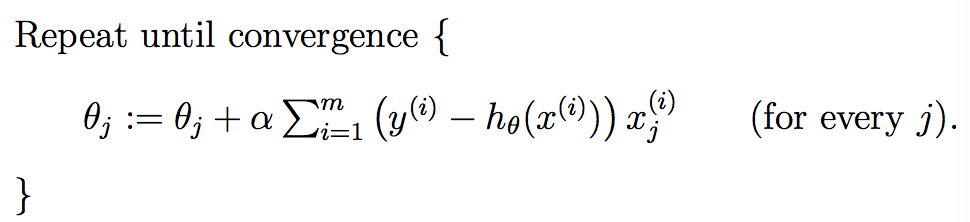
批量梯度下降（batch gradient descent）。

标准方程（normal equations）

矩阵微分（matrix derivatives）

分类和逻辑回归

接下来，我们看看二元分类（binary classification）问题，即预测值y=0或1。0也叫负类（negative class），1则叫正类（positive class）。二元分类中用到的原理同样适用于多元分类。另外，样本(x⁽ⁱ⁾, y⁽ⁱ⁾)中的y⁽ⁱ⁾也叫做类标（label）。

sigmoid函数

广义线性模型（generalized linear models）

softmax回归

参数拟合（parameter fitting），对数似然（log-likelihood）

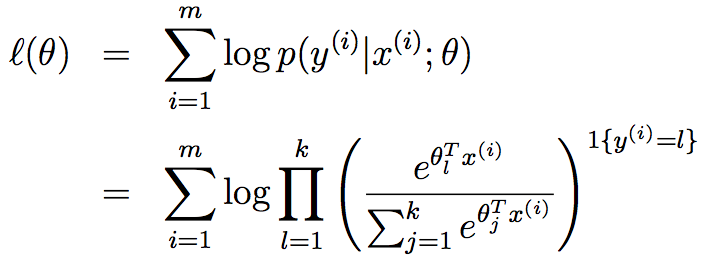
原文链接：

http://cs229.stanford.edu/notes/cs229-notes1.pdf