[leetcode]10. Regular Expression Matching正则表达式的匹配

Given an input string (s) and a pattern (p), implement regular expression matching with support for '.' and '*'.

'.' Matches any single character.
'*' Matches zero or more of the preceding element.

The matching should cover the entire input string (not partial).

Note:

• s could be empty and contains only lowercase letters a-z.
• p could be empty and contains only lowercase letters a-z, and characters like . or *.

Input:
s = "aab"
p = "c*a*b"
Output: true

题意：

'.' any single character.
'*' 0 or more of the preceding element.
whether p can match s ？

Solution1： DP

Step1: 初始化, dp[0][0] = true

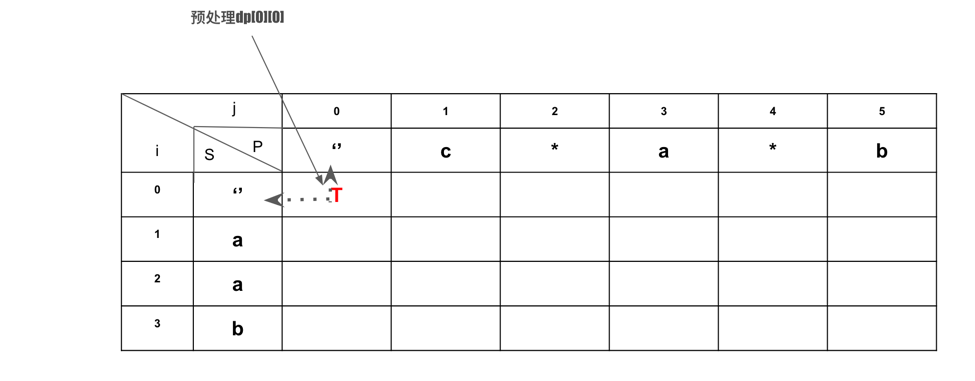
初始化, 是否需要预处理第一个row: dp[0][j] ?  发现当S为空，P为'*' 时，P若取0个preceding element就可能变成空，此时两个字符串match。需要预处理。

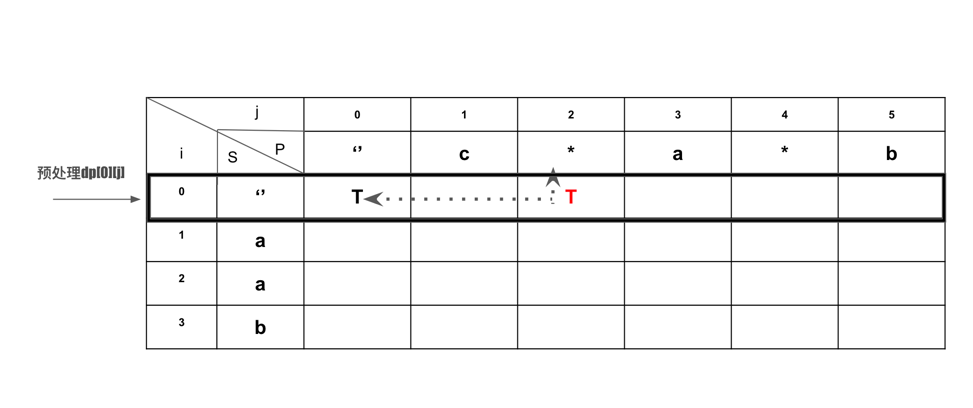
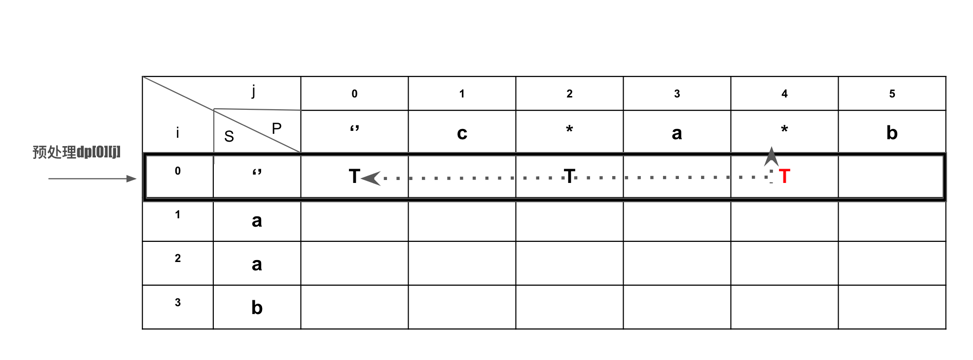
初始化， 是否需要预处理第一个col：dp[i][0]？ 发现当P为空，S为任意字符时，肯定不match。不需要预处理，因为默认default就是false。

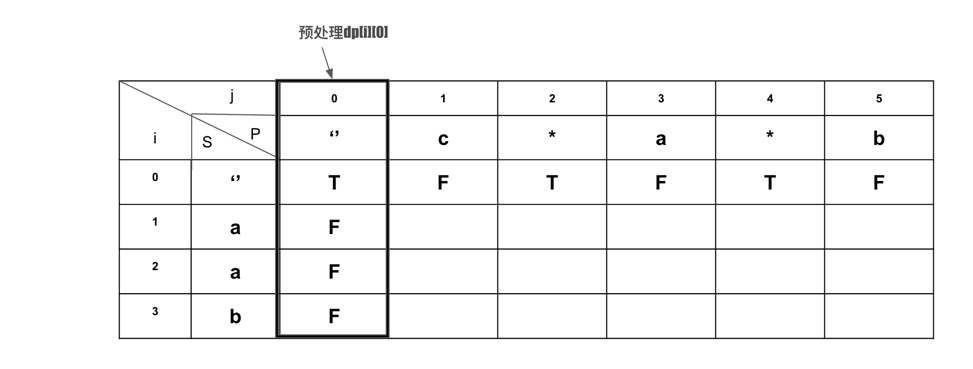
Step2: 找到转移方程，

若两个字符串当前的char不同：

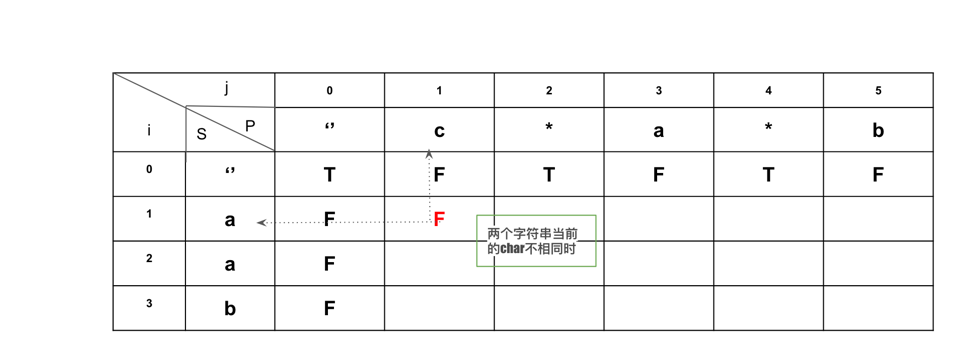
若两个字符串当前的char相同：

p.charAt(j-1) == s.charAt(i-1) or  p.charAt(j-1) == '.'  则当前字符match， 那么dp[i][j] 的结果可以直接拿dp[i-1][j-1]的取值

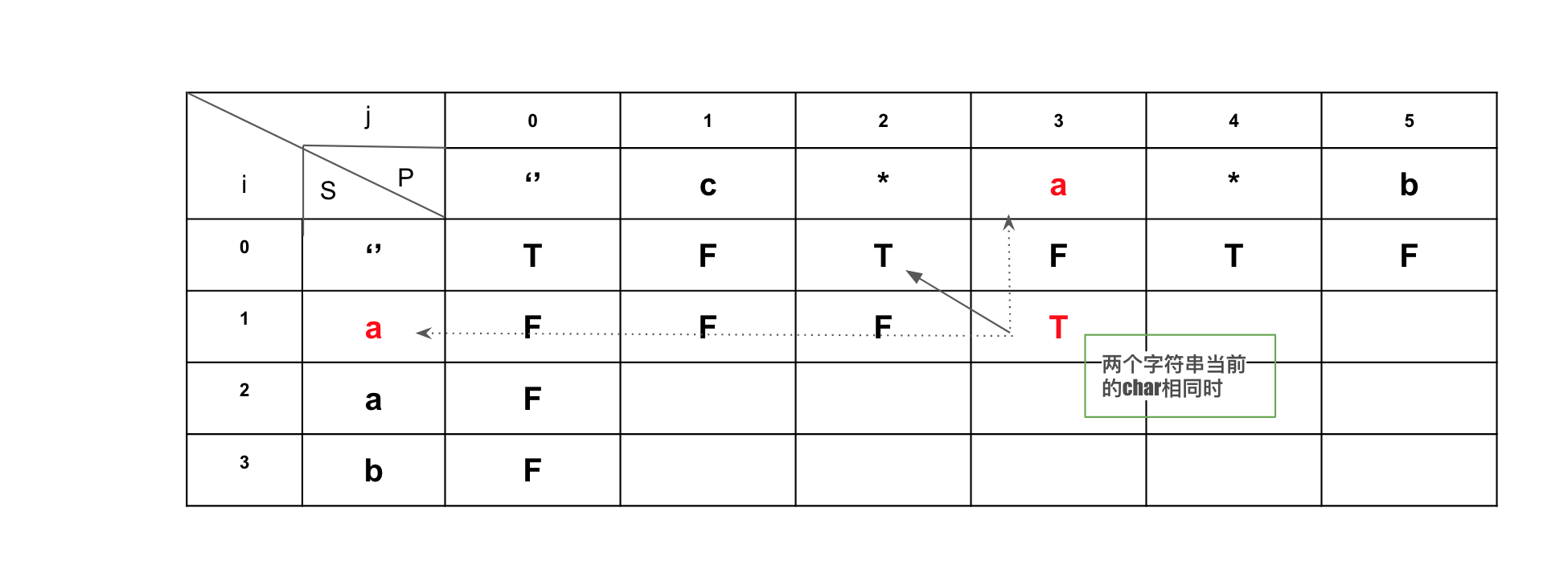
若两个字符串当前的char不同：

1.  p.charAt(j-1) == '*' 时，先退后两步去check一下T/F。因为 "*" 可以消掉其preceding element，dp[i][j] = dp[i][j-2]  【讨论 '*'代表 0 preceding element 】

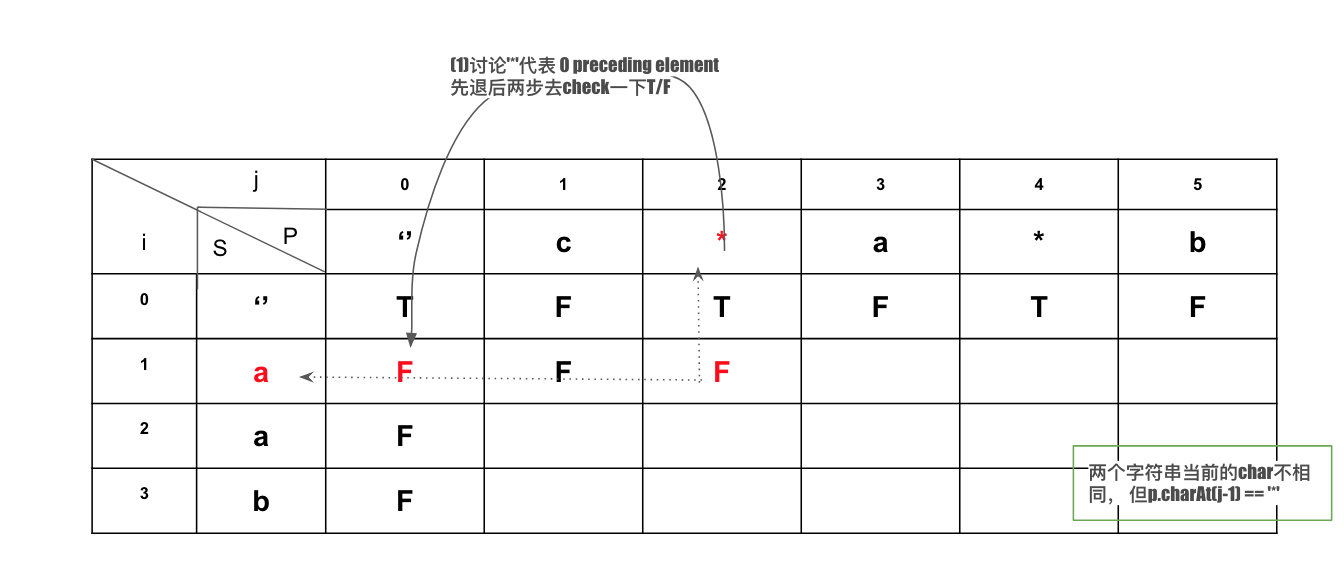
2. p.charAt(j-1) == '*'  且 s.charAt(i-1)  == p.charAt(j-2) || p.charAt(j-2)  == '.' 时 ， 则S当前的字符可以看成是 P的

“ precding element + '*' ” 一部分， 此时可以get rid of S当前的字符， dp[i][j] = dp[i-1][j]   【讨论 '*'代表 1 or more preceding element 】

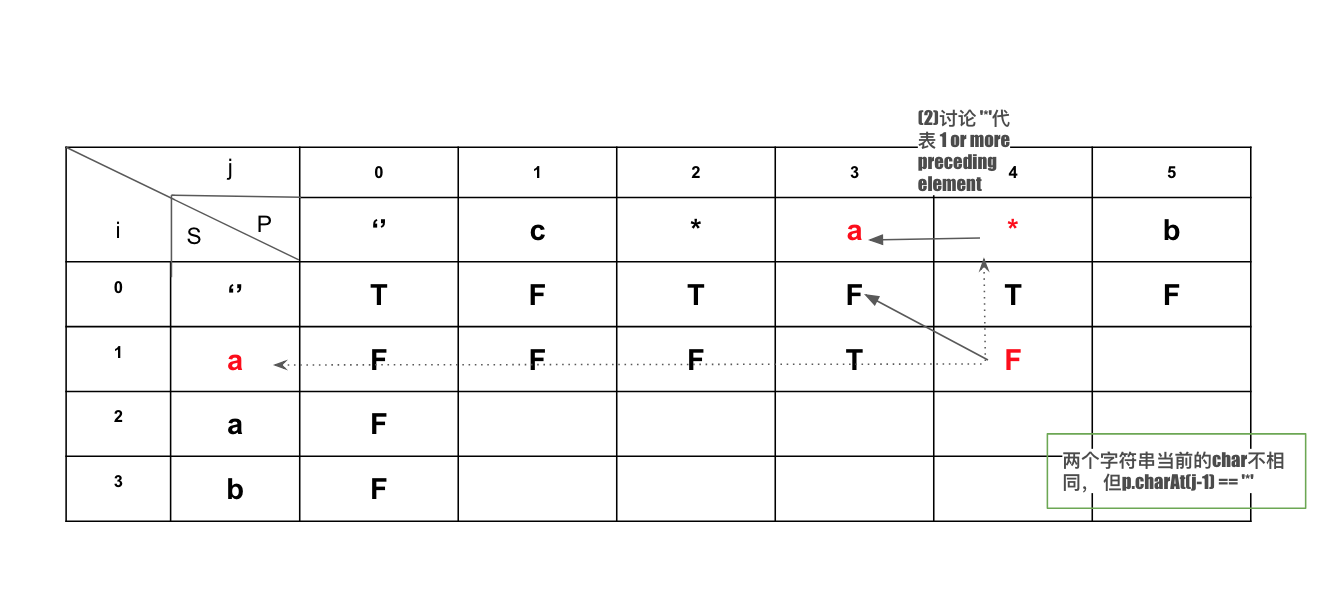
code

 class Solution {
     public boolean isMatch(String s, String p) {
         boolean[][] dp = new boolean[s.length() + 1][p.length() + 1]; // size大小
         dp[0][0] = true;
         for(int j = 1; j<=p.length(); j++){
              if(p.charAt(j-1) == '*') {
                  dp[0][j] = dp[0][j-2] ;
              }
         }

         for(int i = 1; i<=s.length(); i++){
             for(int j = 1; j<=p.length(); j++){
                 if( p.charAt(j-1) == s.charAt(i-1) ||  p.charAt(j-1) == '.' ) {
                      dp[i][j] = dp[i-1][j-1];
                 }else {
                      if( p.charAt(j-1) == '*') {
                          dp[i][j] = dp[i][j-2] ;
                          if (s.charAt(i-1)  == p.charAt(j-2) || p.charAt(j-2)  == '.'){
                              dp[i][j] =  dp[i][j] || dp[i-1][j];
                          }
                      }
                 }
             }
         }
         return dp[s.length()][p.length()];//坐标
     }
 }

注意： 写二维DP，每个人的写code的方法和细节处理不一致。

尤其是为了方便预处理，而多加了空字符' '的二维DP时。

在写code时，很容易弄混到底是dp[s.length()] 还是dp[s.length() + 1]？ 到底是 p.charAt(j) 还是 p.charAt(j-1)？

最好的做法是，严格按照自己画的drawing来写，这样不容易出错！