MATLAB求解非齐次线性方程组

例如方程组：

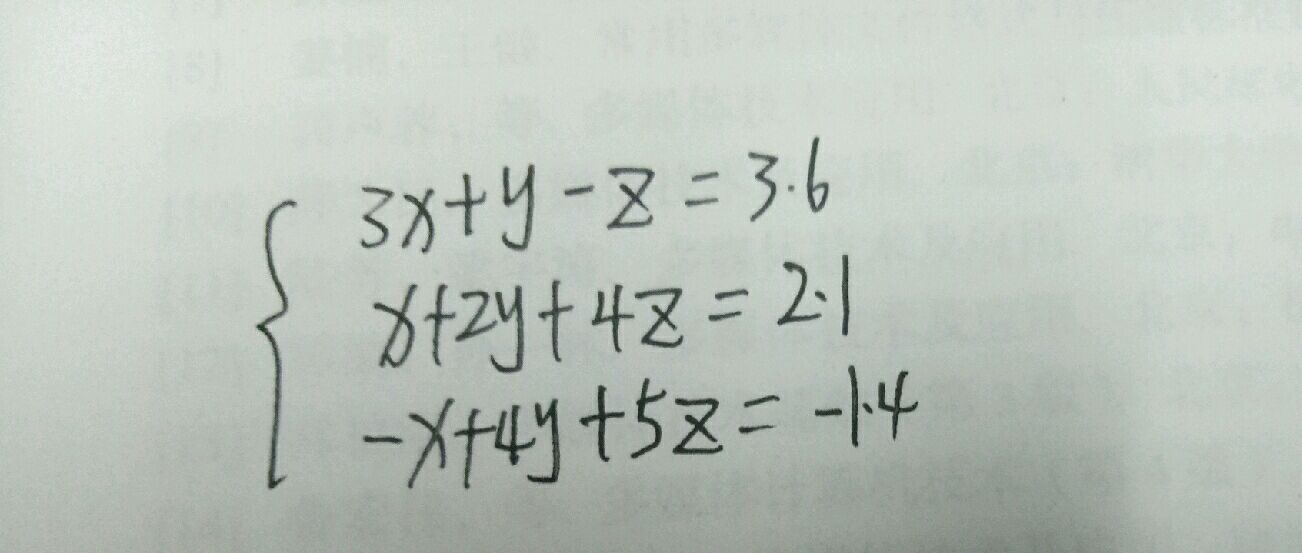
法1：左除法

>> A=[3 1 -1;1 2 4;-1 4 5];b=[3.6;2.1;-1.4];

>> x=A\b

x =

1.4818

-0.4606

0.3848

法2：求逆法

>> A=[3 1 -1;1 2 4;-1 4 5];b=[3.6;2.1;-1.4];

>> x=inv(A)*b

x =

1.4818

-0.4606

0.3848

法3：用linsolve函数求解

>> A=[3 1 -1;1 2 4;-1 4 5];b=[3.6;2.1;-1.4];

>> x=linsolve(A,b)

x =

1.4818

-0.4606

0.3848

法4：用solve函数求解

>> [x1 x2 x3]=solve('3*x1+x2-x3=3.6','x1+2*x2+4*x3=2.1','-x1+4*x2+5*x3=-1.4')

x1 =

1.4818181818181818181818181818182

x2 =

-0.46060606060606060606060606060606

x3 =

0.38484848484848484848484848484848

如果要控制精度，可以使用vpa函数

>> x1=vpa(x1,5)

x1 =

1.4818