树形DP + 换根DP
树形DP——基础
P1352 没有上司的舞会
设 \(f[i][0/1]\) 表示第 \(i\) 个人不去或者去。
如果第 \(i\) 个人没去，那么下属可去可不去，所以 \(f[i][0] = \sum max\{f[j][0],f[j][1]\}\)，\(j\) 为 \(i\) 的子节点。
如果第 \(i\) 个人去了，那么下属不能去，所以 \(f[i][1] = a[i] + \sum f[j][0]\)，\(j\) 为 \(i\) 的子节点。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 6010;
struct Edge {
int to, next;
}e[N * 2];
int head[N], idx;
void add(int a, int b) {
idx++, e[idx].to = b, e[idx].next = head[a], head[a] = idx;
}
int n;
int a[N];
int f[N][2];
void dfs(int u, int fa) {
f[u][1] = a[u];
for (int i = head[u]; i; i = e[i].next) {
int to = e[i].to;
if (to == fa) continue;
dfs(to, u);
f[u][1] += f[to][0];
f[u][0] += max(f[to][0], f[to][1]);
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i < n; i++) {
int a, b;
cin >> a >> b;
add(a, b);
add(b, a);
}
dfs(1, 0);
cout << max(f[1][0], f[1][1]) << '\n';
return 0;
}
POJ 1463 / UVA1292 Strategic game
与上一题类似，
设 \(f[i][0/1]\) 表示第 \(i\) 个人是否驻守。
如果第 \(i\) 个人没去，那么它的儿子必须驻守，所以 \(f[i][0] = 1 + \sum f[j][1]\)，\(j\) 为 \(i\) 的子节点。
如果第 \(i\) 个人去了，那么它的儿子可去可不去，所以 \(f[i][1] = \sum min\{f[j][0],f[j][1]\}\)，\(j\) 为 \(i\) 的子节点。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1510;
struct Edge {
int to, next;
}e[N * 2];
int head[N], idx;
void add(int a, int b) {
idx++, e[idx].to = b, e[idx].next = head[a], head[a] = idx;
}
int n;
int f[N][2];
void dfs(int u, int fa) {
f[u][1] = 1;
for (int i = head[u]; i; i = e[i].next) {
int to = e[i].to;
if (to == fa) continue;
dfs(to, u);
f[u][0] += f[to][1];
f[u][1] += min(f[to][0], f[to][1]);
}
}
void solve() {
memset(f, 0, sizeof(f));
memset(head, 0, sizeof(head));
idx = 0;
for (int i = 1; i <= n; i++) {
int a, num;
scanf("%d:(%d)", &a, &num);
a++;
for (int j = 1; j <= num; j++) {
int b;
scanf("%d", &b);
b++;
add(a, b);
add(b, a);
}
}
dfs(1, 0);
printf("%d\n", min(f[1][0], f[1][1]));
}
int main() {
while (~scanf("%d", &n)) solve();
return 0;
}
P3574 [POI2014] FAR-FarmCraft
设 \(f[i]\) 表示以 \(i\) 为根节点的子树中（包括节点 \(i\)）的所有人安装好游戏所需要的时间（与下面的 \(g[i]\) 并没有包含关系，管理员也没有强制性要求要回到根节点，比如会出现下图情况）。
设 \(g[i]\) 表示从 \(i\) 开始往下走，兜一圈又回到 \(i\) 所需要的时间。
实际上 \(f[i]\) 可能 \(< g[i]\)，比如当出现如下情况的时候：
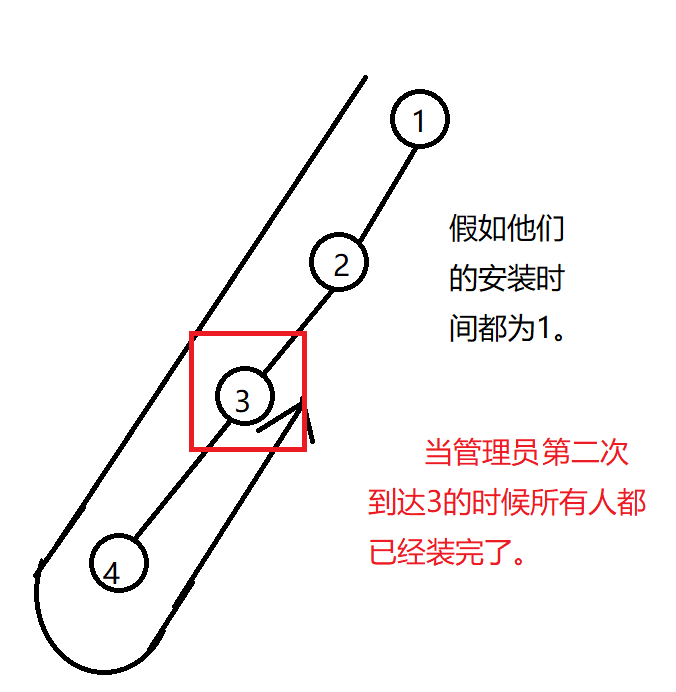
那我们先访问那个节点呢？
分为两种情况考虑，即 \(f[i] - g[i] \geq 0\) 和 \(f[i] - g[i] < 0\) 两种情况。
如果管理员回到了起点那些人还没有装完（即 \(f[i] - g[i] \geq 0\)），那么就需要等待 \(f[i] - g[i]\) 的时间所有人才能安装好。
根据常识，在等待的这段时间我们可以去下一家，以减少所需的总时间。
这里我们利用贪心，让需要等待时间最久的作为第一个访问的节点，
这样可以管理员在他漫长的安装时间内将电脑送给其他人。
而如果出现了像上图一样的情况（即 \(f[i] - g[i] < 0\)） 的情况，
根本就不需要等待，
也就不用排序，
随机访问即可，
但为了简单起见，
排了序也没有什么问题。
所以我们可以对 \(f[i] - g[i]\) 从大到小进行排序。
再挨个访问即可。
然后就是利用 \(f\) 和 \(g\) 来用子树信息更新父亲节点。
如下图：
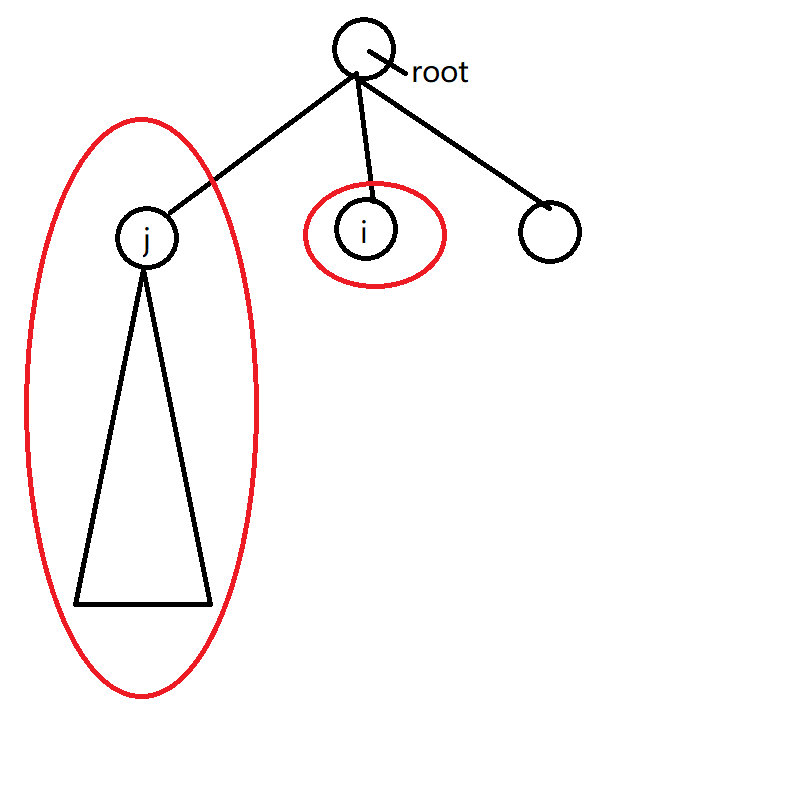
先说结论：只安装到 \(i\) 点会需要 \(\sum (g[j] + 2) + 1 + f[i]\) 的时间能完成安装，其中 \(j\) 为比 \(i\) 先遍历到的同一层的节点（如上图）。
为什么是这样呢？
第一部分的 \(\sum (g[j] + 2)\) 表示遍历完所有 \(j\) 子树的节点，每次都回到根节点（所以要 \(+2\)）。
第二部分的 \(+1\) 表示从根节点走到 \(i\) 所需要的步骤（即为 \(1\) 步）。
最后一部分的 \(f[i]\) 表示把 \(i\) 子树内所有的游戏装好了需要花的时间。
总时间取 \(\max\) 即可， 即 \(f[root] = \max\{\sum (g[j] + 2) + f[i] + 1\}\)。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 500010;
struct Edge {
int to, next;
}e[N * 2];
int head[N], idx;
void add(int a, int b) {
idx++;
e[idx].to = b;
e[idx].next = head[a];
head[a] = idx;
}
int n, t[N];
int f[N], g[N];
void dfs(int u, int fa) {
vector<int> wait;
for (int i = head[u]; i; i = e[i].next) {
int to = e[i].to;
if (to == fa) continue;
dfs(to, u);
wait.push_back(to);
}
sort(wait.begin(), wait.end(), [](const int& a, const int& b) { return f[a] - g[a] > f[b] - g[b]; });
for (int i = 0; i < wait.size(); i++) {
f[u] = max(f[u], g[u] + 1 + f[wait[i]]);
g[u] += g[wait[i]] + 2;
}
if (t[u] > g[u] && u != 1) f[u] = max(f[u], t[u]);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
for (int i = 1; i <= n; i++) cin >> t[i];
for (int i = 1; i < n; i++) {
int a, b;
cin >> a >> b;
add(a, b);
add(b, a);
}
dfs(1, 0);
cout << max(f[1], g[1] + t[1]) << '\n';
return 0;
}
树形DP——树上背包
P2014 CTSC1997 选课
不难发现这是个树结构。
课程相当于树上的每一个节点，
学分相当于权值。
设 \(f[i][j][k]\) 表示遍历到第 \(i\) 棵子树的第 \(j\) 个元素并且选择 \(k\) 个节点可以得到的最大权值。
\(f[cur][i][j] = \max \{f[cur][i - 1][j - l] + f[ver[cur][i]][size[ver[i]]][l]\}\)。
其中 \(ver[i][j]\) 表示 \(i\) 节点的第 \(j\) 个子节点，\(size[x]\) 表示以 \(x\) 为根节点的子树的大小。
然后像01背包一样把第二维滚掉就可以了。
C++代码
版本1：
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 310;
struct Edge {
int to, next;
}e[N * 2];
int head[N], idx;
void add(int a, int b) {
idx++;
e[idx].to = b;
e[idx].next = head[a];
head[a] = idx;
}
int n, m;
int sz[N];
int a[N];
int f[N][N];
void dfs(int u) {
sz[u] = 1;
f[u][1] = a[u];
for (int i = head[u]; i; i = e[i].next) {
int to = e[i].to;
dfs(to);
sz[u] += sz[to];
for (int j = min(sz[u], m + 1); j >= 1; j--) {
for (int k = 1; k <= min(sz[to], j - 1); k++) {
f[u][j] = max(f[u][j], f[u][j - k] + f[to][k]);
}
}
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
for (int i = 1; i <= n; i++) {
int b;
cin >> b >> a[i];
add(b, i);
}
dfs(0);
cout << f[0][m + 1] << '\n';
return 0;
}
版本2：
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 310;
struct Edge {
int to, next;
}e[N * 2];
int head[N], idx;
void add(int a, int b) {
idx++;
e[idx].to = b;
e[idx].next = head[a];
head[a] = idx;
}
int n, m;
int sz[N];
int a[N];
int f[N][N];
void dfs(int u) {
sz[u] = 1;
f[u][1] = a[u];
for (int i = head[u]; i; i = e[i].next) {
int to = e[i].to;
dfs(to);
for (int j = min(sz[u], m + 1); j >= 1; j--) {
for (int k = 1; k <= sz[to] && j + k <= m + 1; k++) {
f[u][j + k] = max(f[u][j + k], f[u][j] + f[to][k]);
}
}
sz[u] += sz[to];
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
for (int i = 1; i <= n; i++) {
int b;
cin >> b >> a[i];
add(b, i);
}
dfs(0);
cout << f[0][m + 1] << '\n';
return 0;
}
P4516 [JSOI2018] 潜入行动
设 \(f[i][j][0/1][0/1]\) 表示在以 \(i\) 为根节点的子树中除节点 \(i\) 的全部节点被覆盖而且使用了 \(j\) 个监听设备时节点 \(i\) 的状况，第一个 \([0/1]\) 表示有没有放置监听设备，第二个 \([0/1]\) 表示 \(i\) 有没有被覆盖。
有：
\(f[u][i + j][0][0] = \sum f[u][i][0][0] \times f[v][j][0][1]\)
\(f[u][i + j][0][1] = \sum f[u][i][0][1] \times (f[v][j][0][1] + f[v][j][1][1]) + f[u][i][0][0] \times f[v][j][1][1]\)
\(f[u][i + j][1][0] = \sum f[u][i][1][0] \times (f[v][j][0][0] + f[v][j][0][1])\)
\(f[u][i + j][1][1] = \sum f[u][i][1][1] \times (f[v][j][0][0] + f[v][j][0][1] + f[v][j][1][0] + f[v][j][1][1]) + f[u][i][1][0] \times (f[v][j][1][0] + f[v][j][1][1])\)
注意：
1. 每次计算时都要把 \(f[u]\) 清空重新统计，所以只能用 \(tmp\) 数组当一下“替身 ”了。*
2. 此题卡空间、时间。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
using namespace std;
const int N = 100010, M = 110, mod = 1000000007;
struct Edge {
int to, next;
}e[N * 2];
int head[N], idx;
void add(int a, int b) {
idx++;
e[idx].to = b;
e[idx].next = head[a];
head[a] = idx;
}
struct num {
int x;
num operator+(num b) {
while (b.x >= mod) b.x -= mod;
long long tmp = 1ll * x + b.x;
while (tmp >= mod) tmp -= mod;
num res;
res.x = tmp;
return res;
}
void operator+=(num b) {
while (b.x >= mod) b.x -= mod;
long long tmp = 1ll * x + b.x;
while (tmp >= mod) tmp -= mod;
x = tmp;
}
num operator*(num b) {
num res;
res.x = (1ll * x * b.x) % mod;
return res;
}
void operator=(int k) {
x = k;
}
};
int n, k;
int sz[N];
num f[N][M][2][2];
num t[M][2][2];
void dfs(int u, int fa) {
sz[u] = 1;
f[u][0][0][0] = 1;
f[u][1][1][0] = 1;
for (int tmp = head[u]; tmp; tmp = e[tmp].next) {
int v = e[tmp].to;
if (v == fa) continue;
dfs(v, u);
memcpy(t, f[u], sizeof(t));
memset(f[u], 0, sizeof(f[u]));
for (int i = min(sz[u], k); i >= 0; i--) {
for (int j = 0; j <= min(sz[v], k - i); j++) {
f[u][i + j][0][0] += t[i][0][0] * f[v][j][0][1];
f[u][i + j][0][1] += t[i][0][1] * (f[v][j][0][1] + f[v][j][1][1]) + t[i][0][0] * f[v][j][1][1];
f[u][i + j][1][0] += t[i][1][0] * (f[v][j][0][0] + f[v][j][0][1]);
f[u][i + j][1][1] += t[i][1][1] * (f[v][j][0][0] + f[v][j][0][1] + f[v][j][1][0] + f[v][j][1][1]) + t[i][1][0] * (f[v][j][1][0] + f[v][j][1][1]);
}
}
sz[u] += sz[v];
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> k;
for (int i = 1; i < n; i++) {
int x, y;
cin >> x >> y;
add(x, y);
add(y, x);
}
dfs(1, 0);
cout << (f[1][k][0][1] + f[1][k][1][1]).x << '\n';
return 0;
}
换根DP
换根法思路：
- 自下而上递推；
- 自上而下递推。
P3478 [POI2008] STA-Station
题目描述：
思路：
个节点 \(u\) 为根的子树大小 \(s[u]\)。
然后我们设 \(f[i]\) 为以 \(i\) 为根时所有节点的深度之和，\(j\) 为 \(i\) 的子节点。
那么对于所有 \(j\) 的子节点，深度都减 \(1\)，所以总共减少了 \(s[j]\)。
对于所有不是 \(j\) 的子节点的节点，深度都加 \(1\) ，所以总共加了 \(n - s[j]\)。
所以 \(f[j] = f[i] - s[j] + n - s[j] = f[i] + n - 2 \times s[j]\)。
最后取 \(\max\) 即可。
代码：
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
using i64 = long long;
const int N = 1000010;
struct Edge {
int to, next;
}e[N * 2];
int head[N], idx;
void add(int a, int b) {
idx++;
e[idx].to = b;
e[idx].next = head[a];
head[a] = idx;
}
int n;
int sz[N];
void dfs1(int u, int fa) {
sz[u] = 1;
for (int i = head[u]; i; i = e[i].next) {
int to = e[i].to;
if (to == fa) continue;
dfs1(to, u);
sz[u] += sz[to];
}
}
int f[N];
int maxv, ans;
void dfs2(int u, int fa) {
for (int i = head[u]; i; i = e[i].next) {
int to = e[i].to;
if (to == fa) continue;
f[to] = f[u] + n - 2 * sz[to];
dfs2(to, u);
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
for (int i = 1; i < n; i++) {
int x, y;
cin >> x >> y;
add(x, y);
add(y, x);
}
dfs1(1, 0);
for (int i = 1; i <= n; i++) f[1] += sz[i];
dfs2(1, 0);
for (int i = 1; i <= n; i++) if (f[i] > maxv) maxv = f[i], ans = i;
cout << ans << '\n';
return 0;
}
AcWing 287. 积蓄程度 / POJ 3585 Accumulation Degree
题目描述：
思路：
设 \(d[i]\) 表示 \(i\) 点可以向下传递的最大流量。
设 \(f[i]\) 表示 \(i\) 点可以向外传递的最大流量（包括向下流的流量和向上流的流量）。
先 \(\text{dfs}\) 一遍求出 \(d\)。
有：
如无特殊说明 \(to\) 表示 \(i\) 的子节点，\(edge(i, to)\) 表示 \(i\) 和 \(to\) 这条边的最大流量。
\(d[i] = \sum \min(d[to], edge(i, to))\)
\(f[to] = \min(edge(i, to), f[i] - \min(edge(i, to), d[to]))\)
同时注意如果根的度为 \(1\)（如下图） ，那么计算它的子节点时要采用公式：
\(f[i] = f[to] + edge(i, to)\)
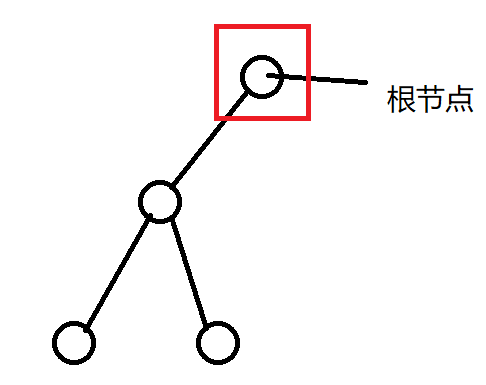
代码：
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 200010, INF = 0x3f3f3f3f;
struct Edge {
int to;
int next;
int w;
}e[N * 2];
int head[N], idx, deg[N];
void add(int a, int b, int c) {
idx++;
e[idx].to = b;
e[idx].next = head[a];
e[idx].w = c;
head[a] = idx;
}
int n;
int f[N], d[N];
int dfs1(int u, int fa) {
for (int i = head[u]; i; i = e[i].next) {
int to = e[i].to;
if (to == fa) continue;
d[u] += min(dfs1(to, u), e[i].w);
}
if (deg[u] == 1) return INF;
return d[u];
}
void dfs2(int u, int fa) {
for (int i = head[u]; i; i = e[i].next) {
int to = e[i].to;
if (to == fa) continue;
if (deg[u] == 1) f[to] = d[to] + e[i].w;
else f[to] = d[to] + min(e[i].w, f[u] - min(d[to], e[i].w));
dfs2(to, u);
}
}
void solve() {
idx = 0;
memset(head, 0, sizeof(head));
memset(deg, 0, sizeof(deg));
memset(f, 0, sizeof(f));
memset(d, 0, sizeof(d));
cin >> n;
for (int i = 1; i < n; i++) {
int x, y, z;
cin >> x >> y >> z;
add(x, y, z);
add(y, x, z);
deg[x]++;
deg[y]++;
}
dfs1(1, 0);
f[1] = d[1];
dfs2(1, 0);
int ans = 0;
for (int i = 1; i <= n; i++) ans = max(ans, f[i]);
cout << ans << '\n';
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
cin >> T;
while (T--) solve();
return 0;
}
P2986 [USACO10MAR] Great Cow Gathering G
题目描述：
思路：
设 \(f[u]\) 表示如果选择集会的地点为 \(u\) 点时所需时间。
根据经验，我们可以得到
\(f[to] = f[u] - to\text{节点下所有奶牛个数} \times w(u, to) + (奶牛总数 - to\text{节点下所有奶牛个数}) \times w(u, to)\)。
代码：
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 100010, M = 200010;
struct Edge {
int to;
int next;
int w;
}e[M];
int head[N], idx;
void add(int a, int b, int c) {
idx++;
e[idx].to = b;
e[idx].next = head[a];
e[idx].w = c;
head[a] = idx;
}
int sz[N];
int cnt[N];
int dfs(int u, int fa) {
int all = 0;
sz[u] = cnt[u];
for (int i = head[u]; i; i = e[i].next) {
int to = e[i].to;
if (to == fa) continue;
all += dfs(to, u);
sz[u] += sz[to];
all += sz[to] * e[i].w;
}
return all;
}
int f[N], n, get_n;
void dfs2(int u, int fa) {
for (int i = head[u]; i; i = e[i].next) {
int to = e[i].to;
if (to == fa) continue;
f[to] = f[u] - sz[to] * e[i].w + (get_n - sz[to]) * e[i].w;
dfs2(to, u);
}
}
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
for (int i = 1; i <= n; i++) cin >> cnt[i], get_n += cnt[i];
for (int i = 1; i < n; i++) {
int x, y, z;
cin >> x >> y >> z;
add(x, y, z);
add(y, x, z);
}
f[1] = dfs(1, 0);
dfs2(1, 0);
int min_sum = 0x3f3f3f3f3f3f3f3f;
for (int i = 1; i <= n; i++) {
if (min_sum > f[i]) {
min_sum = f[i];
// ans = i;
}
}
cout << min_sum << '\n';
return 0;
}
P3047 [USACO12FEB]Nearby Cows G
题目描述
思路
使用换根DP，
设 \(dp[i][j]\) 表示以 \(i\) 为根节点的子树中深度小于等于 \(j\) 的点的权值之和。
设 \(f[i][j]\) 表示将第 \(i\) 个点作为整棵树的根节点深度小于等于 \(j\) 的点的权值之和。
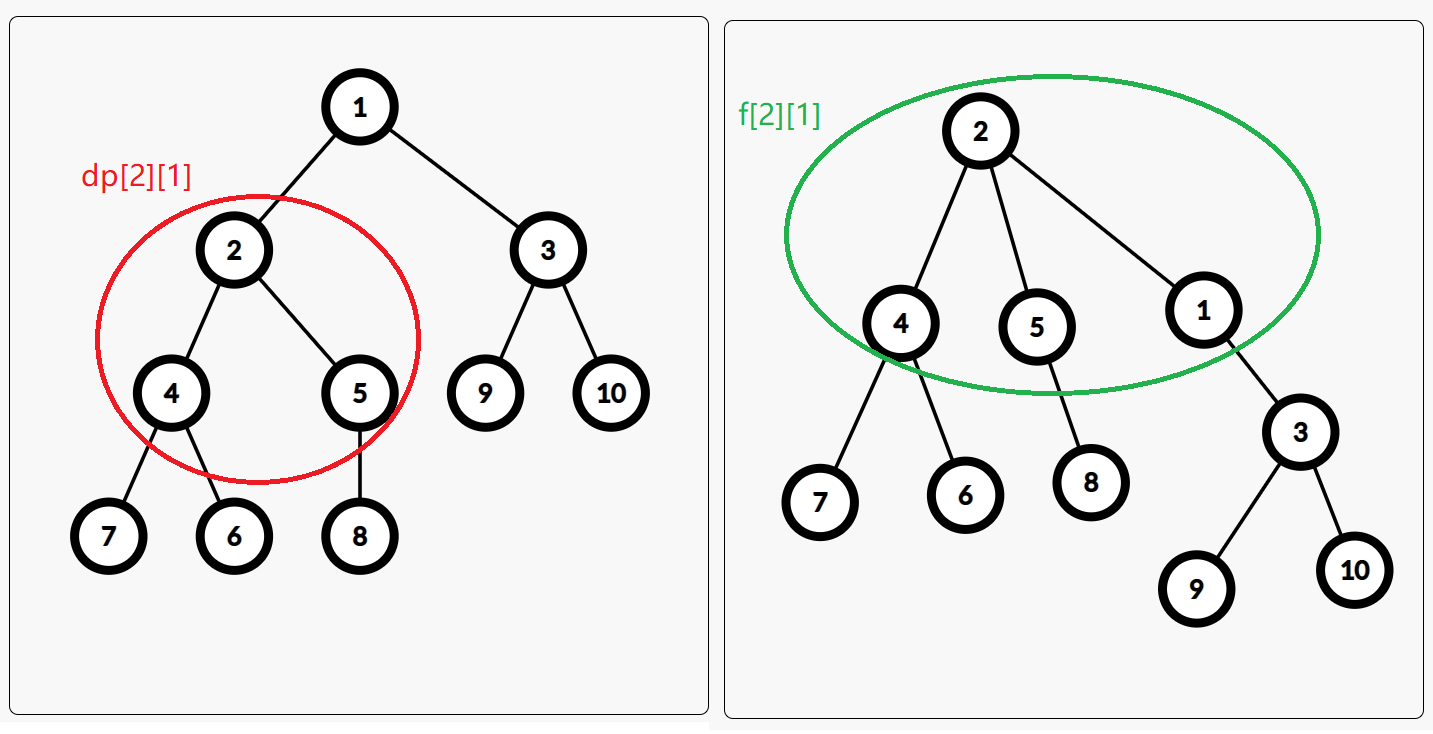
有：
dp[u][k] = \sum dp[to][k - 1] \\
f[to][j] = dp[to][j] - dp[to][j - 2] + f[u][j - 1]
\end{cases}
\]
\(f[to][j] = dp[to][j] - dp[to][j - 2] + f[u][j - 1]\) 表示：
代码：
#include <bits/stdc++.h>
using namespace std;
const int N = 100010, M = 30;
int w[N];
struct Edge {
int to;
int next;
}e[N * 2];
int head[N], idx;
void add(int a, int b) {
idx++;
e[idx].to = b;
e[idx].next = head[a];
head[a] = idx;
}
int n, k;
int dp[N][M];
int f[N][M];
void dfs(int u, int fa) {
for (int i = 0; i <= k; i++) dp[u][i] = w[u];
for (int i = head[u]; i; i = e[i].next) {
int to = e[i].to;
if (to == fa) continue;
dfs(to, u);
for (int i = 1; i <= k; i++) dp[u][i] += dp[to][i - 1];
}
}
void dfs2(int u, int fa) {
for (int i = head[u]; i; i = e[i].next) {
int to = e[i].to;
if (to == fa) continue;
f[to][1] = dp[to][1] + w[u];
for (int j = k; j >= 2; j--) f[to][j] = f[u][j - 1] - dp[to][j - 2] + dp[to][j];
dfs2(to, u);
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> k;
for (int i = 1; i < n; i++) {
int a, b;
cin >> a >> b;
add(a, b);
add(b, a);
}
for (int i = 1; i <= n; i++) cin >> w[i];
dfs(1, 0);
memcpy(f[1], dp[1], sizeof(f[1]));
dfs2(1, 0);
for (int i = 1; i <= n; i++) cout << f[i][k] << '\n';
return 0;
}
树形DP + 换根DP的更多相关文章
- bzoj 3743 [Coci2015]Kamp——树形dp+换根
题目:https://www.lydsy.com/JudgeOnline/problem.php?id=3743 树形dp+换根. “从根出发又回到根” 减去 “mx ” . 注意dfsx里真的要改那 ...
- 模拟赛：树和森林(lct.cpp) （树形DP，换根DP好题）
题面 题解 先解决第一个子问题吧,它才是难点 Subtask_1 我们可以先用一个简单的树形DP处理出每棵树内部的dis和,记为dp0[i], 然后再用一个换根的树形DP处理出每棵树内点 i 到树内每 ...
- 树形dp换根，求切断任意边形成的两个子树的直径——hdu6686
换根dp就是先任取一点为根,预处理出一些信息,然后在第二次dfs过程中进行状态的转移处理 本题难点在于任意割断一条边,求出剩下两棵子树的直径: 设割断的边为(u,v),设down[v]为以v为根的子树 ...
- POJ 3585 Accumulation Degree【换根DP】
传送门:http://poj.org/problem?id=3585 题意:给定一张无根图,给定每条边的容量,随便取一点使得从这个点出发作为源点,发出的流量最大,并且输出这个最大的流量. 思路:最近开 ...
- 【换根DP】小奇的仓库
题目背景 小奇采的矿实在太多了,它准备在喵星系建个矿石仓库.令它无语的是,喵星系的货运飞船引擎还停留在上元时代! 题目内容 喵星系有\(n\)个星球,星球以及星球间的航线形成一棵树. 从星球\(a\) ...
- [倍增][换根DP]luogu P5024 保卫王国
题面 https://www.luogu.com.cn/problem/P5024 分析 可以对有限制的点对之间的链进行在倍增上的DP数组合并. 需要通过一次正向树形DP和一次换根DP得到g[0][i ...
- [BZOJ4379][POI2015]Modernizacja autostrady[树的直径+换根dp]
题意 给定一棵 \(n\) 个节点的树,可以断掉一条边再连接任意两个点,询问新构成的树的直径的最小和最大值. \(n\leq 5\times 10^5\) . 分析 记断掉一条边之后两棵树的直径为 \ ...
- 2018.10.15 NOIP训练 水流成河（换根dp）
传送门 换根dp入门题. 貌似李煜东的书上讲过? 不记得了. 先推出以1为根时的答案. 然后考虑向儿子转移. 我们记f[p]f[p]f[p]表示原树中以ppp为根的子树的答案. g[p]g[p]g[p ...
- 换根DP+树的直径【洛谷P3761】 [TJOI2017]城市
P3761 [TJOI2017]城市 题目描述 从加里敦大学城市规划专业毕业的小明来到了一个地区城市规划局工作.这个地区一共有ri座城市,<-1条高速公路,保证了任意两运城市之间都可以通过高速公 ...
- 小奇的仓库：换根dp
一道很好的换根dp题.考场上现场yy十分愉快 给定树,求每个点的到其它所有点的距离异或上m之后的值,n=100000,m<=16 只能线性复杂度求解,m又小得奇怪.或者带一个log像kx一样打一 ...
随机推荐
- Centos7.x jmeter + ant + jenkins接口自动化框架部署
一.基础环境准备 1.jmeter安装(之前文章有介绍过) 2.ant安装 · 官网下载:https://ant.apache.org/bindownload.cgi · 上传服务器,执行 tar - ...
- Netty服务端开发及性能优化
作者:京东物流 王奕龙 Netty是一个异步基于事件驱动的高性能网络通信框架,可以看做是对NIO和BIO的封装,并提供了简单易用的API.Handler和工具类等,用以快速开发高性能.高可靠性的网络服 ...
- Istio数据面新模式：Ambient Mesh技术解析
摘要:Ambient Mesh以一种更符合大规模落地要求的形态出现,克服了大多数Sidecar模式的固有缺陷,让用户无需再感知网格相关组件,真正将网格下沉为基础设施. 本文分享自华为云社区<华为 ...
- 武装你的WEBAPI-OData与DTO
前面写了很多有关OData使用的文章,很多读者会有疑问,直接将实体对象暴露给最终用户会不会有风险?$expand在默认配置的情况下,数据会不会有泄露风险? 答案是肯定的,由于OData的特性,提供给我 ...
- vue全家桶进阶之路1：前言
Vue.js简称Vue,用于构建用户界面的渐进式框架. Vue是一款国产前端框架,它的作者尤雨溪(Evan You)是一位美籍华人,2014年2月,尤雨溪开源了一个前端开发库 Vue.js,2015年 ...
- 数据分析缺失值处理(Missing Values)——删除法、填充法、插值法
缺失值指数据集中某些变量的值有缺少的情况,缺失值也被称为NA(not available)值.在pandas里使用浮点值NaN(Not a Number)表示浮点数和非浮点数中的缺失值,用NaT表示时 ...
- itextpdf5.5.13给pdf添加图片水印、添加文字水印（平铺）、添加文字水印（单个）、添加页眉、页脚、页眉事件、添加图片
转载自简书用户:alex很累,感谢分享.原地址:https://www.jianshu.com/p/2b9c7a0300e4 一.相关工具类 1. Excel2Pdf.java (如代码不可用请查看原 ...
- 从 pheatmap 无缝迁移至 ComplexHeatmap
pheatmap 是一个非常受欢迎的绘制热图的 R 包.ComplexHeatmap 包即是受之启发而来.你可以发现Heatmap()函数中很多参数都与pheatmap()相同.在 pheatmap ...
- Anaconda入门使用指南（一）
python 是目前最流程的编程语言之一,但对于很多初学者而言,python 的包.环境以及版本的管理却是一个令人头疼的问题,特别是对于使用 Windows 的童鞋.为了解决这些问题,有不少发行版的 ...
- UpSetR：多数据集绘图可视化处理利器
说到集合数据可视化,我们第一时间想到的就是韦恩图.在 NGS 相关的研究中,韦恩图用来直观表征不同的集合之间元素重叠关系,是经常在文献中出现的图. 在集合数少的时候韦恩图是很好用的,但是当集合数多比如 ...