准备NOIP2017 最长公共子序列（模版）

一些概念：

（1）子序列： 一个序列A ＝ a1,a2,……an,中任意删除若干项，剩余的序列叫做A的一个子序列。也可以认为是从序列A按原顺序保留任意若干项得到的序列。

例如：

 

对序列 1,3,5,4,2,6,8,7来说，序列3,4,8,7 是它的一个子序列。
对于一个长度为n的序列，它一共有2^n 个子序列，有(2^n – 1)个非空子序列。

请注意：子序列不是子集，它和原始序列的元素顺序是相关的。

（2）公共子序列 ： 顾名思义，如果序列C既是序列A的子序列，同时也是序列B的子序列，则称它为序列A和序列B的公共子序列。

例如：

 

对序列 1,3,5,4,2,6,8,7和序列 1,4,8,6,7,5 来说

序列1,8,7是它们的一个公共子序列。

请注意： 空序列是任何两个序列的公共子序列。

例如： 序列1,2,3和序列4,5,6的公共子序列只有空序列。

 

（3）最长公共子序列

A和B的公共子序列中长度最长的（包含元素最多的）叫做A和B的公共子序列。
仍然用序列1,3,5,4,2,6,8,7和序列1,4,8,6,7,5

它们的最长公共子序列是：

1,4,8,7
1,4,6,7

最长公共子序列的长度是4 。
请注意: 最长公共子序列不唯一。

请大家用集合的观点来理解这些概念，子序列、公共子序列以及最长公共子序列都不唯一，所以我们通常说一个最长公共子序列，但显然最长公共子序列的长度是一定的。

最长公共子序列问题就是求序列A= a1,a2,……an, 和B = b1,b2,……bm,的一个最长公共子序列。

因为最长公共子序列不唯一，让我们把问题简化，如何求出两个序列的最长公共子序列长度呢？

你首先能想到的恐怕是暴力枚举？那我们先来看看：序列A有 2^n 个子序列，序列B有 2^m 个子序列，如果任意两个子序列一一比较，比较的子序列高达 2^(n+m) 对，这还没有算具体比较的复杂度。

或许你说，只有长度相同的子序列才会真正进行比较。那么忽略空序列，我们来看看：对于A长度为1的子序列有C(n,1)个，长度为2的子序列有C(n,2)个，……长度为n的子序列有C(n,n)个。对于B也可以做类似分析，即使只对序列A和序列B长度相同的子序列做比较，那么总的比较次数高达：

C(n,1)*C(m,1)*1 + C(n,2) * C(m,2) * 2+ …+C(n,p) * C(m,p)*p

其中p = min(m, n)。

吓着了吧？怎么办？试试使用动态规划算法！

我们用Ax表示序列A的连续前x项构成的子序列，即Ax= a1,a2,……ax, By= b1,b2,……by, 我们用LCS(x, y)表示它们的最长公共子序列长度，那原问题等价于求LCS(m,n)。为了方便我们用L(x, y)表示Ax和By的一个最长公共子序列。

让我们来看看如何求LCS(x, y)。我们令x表示子序列考虑最后一项

（1） Ax ＝ By

那么它们L(Ax, By)的最后一项一定是这个元素！

为什么呢？为了方便，我们令t = Ax = By, 我们用反证法：假设L(x,y)最后一项不是t，

则要么L(x,y)为空序列（别忘了这个），要么L(x,y)的最后一项是Aa＝Bb ≠ t, 且显然有a < x, b < y。无论是哪种情况我们都可以把t接到这个L(x,y)后面,从而得到一个更长的公共子序列。矛盾！

如果我们从序列Ax中删掉最后一项ax得到Ax-1,从序列By中也删掉最后一项by得到By-1，(多说一句角标为0时，认为子序列是空序列)，则我们从L(x,y)也删掉最后一项t得到的序列是L(x – 1, y - 1)。为什么呢？和上面的道理相同，如果得到的序列不是L(x - 1, y - 1)，则它一定比L(x - 1, y - 1)短（注意L（，）是个集合！），那么它后面接上元素t得到的子序列L(x,y)也比L(x - 1, y - 1)接上元素t得到的子序列短，这与L(x, y)是最长公共子序列矛盾。

 

因此L(x, y) = L(x - 1, y - 1) 最后接上元素t

LCS(Ax, By) = LCS(x - 1, y - 1) + 1

（2）  Ax ≠ By

仍然设t = L(Ax, By), 或者L(Ax, By)是空序列（这时t是未定义值不等于任何值）。

则t  ≠ Ax和t  ≠ By至少有一个成立，因为t不能同时等于两个不同的值嘛！

（2.1） 如果t  ≠ Ax，则有L(x, y)= L(x - 1, y)，因为根本没Ax的事嘛。

 LCS(x,y) = LCS(x – 1, y)

（2.2） 如果t  ≠ By,l类似L(x, y)= L(x , y - 1)

LCS(x,y) = LCS(x, y – 1)

可是，我们事先并不知道t，由定义，我们取最大的一个，因此这种情况下,有LCS(x,y) = max(LCS(x – 1, y) , LCS(x, y – 1))。
看看目前我们已经得到了什么结论：

LCS(x,y) = 
(1) LCS(x - 1,y - 1) + 1 如果Ax ＝ By
(2) max(LCS(x – 1, y) , LCS(x, y – 1)) 如果Ax ≠ By

这时一个显然的递推式，光有递推可不行，初值是什么呢？

显然，一个空序列和任何序列的最长公共子序列都是空序列！所以我们有:

 

LCS(x,y) = 
(1) LCS(x - 1,y - 1) + 1 如果Ax ＝ By
(2) max(LCS(x – 1, y) , LCS(x, y – 1)) 如果Ax ≠ By
(3) 0 如果x = 0或者y = 0

到此我们求出了计算最长公共子序列长度的递推公式。我们实际上计算了一个(n + 1)行(m + 1)列的表格（行是0..n，列是0..m)，也就这个二维度数组LCS(,)。

大概的伪代码如下：
输入序列A, B长度分别为n，m,计算二维表 LCS(int,int):

for x = 0 to n do
　　for y = 0 to m do
　　　　if (x == 0 || y == 0) then 　
　　　　　　LCS(x, y) = 0
　　　　else if (Ax == By) then
　　　　　　LCS(x, y) = LCS(x - 1,y - 1) + 1
　　　　else
　　　　　　LCS(x, y) = ) max(LCS(x – 1, y) , LCS(x, y – 1))　
　　　　endif
　　endfor
endfor

注意： 我们这里使用了循环计算表格里的元素值，而不是递归，如果使用递归需要已经记录计算过的元素，防止子问题被重复计算。

现在问题来了，我们如何得到一个最长公共子序列而仅仅不是简单的长度呢？其实我们离真正的答案只有一步之遥！

 

仍然考虑那个递推式，我们LCS(x,y)的值来源的三种情况：

（1） LCS(x – 1,  y – 1) + 1如果Ax ＝ By
这对应L(x,y) = L(x,- 1 y- 1)末尾接上Ax

（2.1） LCS(x – 1, y)  如果Ax ≠ By且LCS(x – 1, y) ≥LCS(x, y – 1)
这对应L(x,y)= L(x – 1, y)
（2.2） LCS(x, y – 1)  如果Ax ≠ By且LCS(x – 1, y) <LCS(x, y – 1)
这对应L(x,y) = L(x, y – 1)

（3） 0 如果 x =0或者y = 0
这对应L(x,y)=空序列

注意(2.1)和(2.2) ，当LCS(x – 1, y) ＝ LCS(x, y – 1)时，其实走哪个分支都一样，虽然长度时一样的，但是可能对应不同的子序列，所以最长公共子序列并不唯一。
神奇吧？又一个类似的递推公式。可见我们在计算长度LCS(x,y)的时候只要多记录一些信息，就可以利用这些信息恢复出一个最长公共子序列来。就好比我们在迷宫里走路，走到每个位置的时候记录下我们时从哪个方向来的，就可以从终点回到起点一样。

另外，说一下复杂度？

时间复杂度时O(n * m)，空间也是O(n * m)
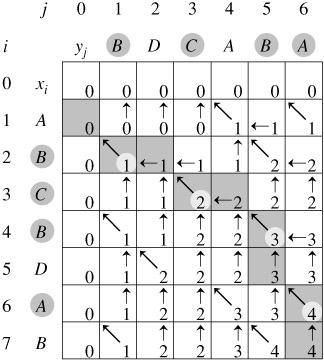
今天对LCS的讲解就到这里，聪明的你是不是已经蠢蠢欲动要AC问题啦？ 心动不如行动，赶快吧。

最后，我们来提供输入输出数据，由你来写一段程序，实现这个算法，只有写出了正确的程序，才能继续后面的课程。

 

输入

第1行：字符串A
第2行：字符串B
(A,B的长度 <= 1000)

输出

 

输出最长的子序列，如果有多个，随意输出1个。

 

输入示例

abcicba
abdkscab

输出示例

abca
代码 

#include<iostream>
#include<cstring>
#include<string>

using namespace std;

string ans[],a,b;
int w,i,j,dp[][];
int main()
{
    cin>>a>>b;
    for(i=;i<=a.length() ;++i)
    {
        for(j=;j<=b.length() ;++j)
        {
            if(a[i-]==b[j-]) dp[i][j]=dp[i-][j-]+;
            else {
                if(dp[i][j-]>=dp[i-][j])
                dp[i][j]=dp[i][j-];
                else dp[i][j]=dp[i-][j];
            }
        }
    }
    for(i=a.length(),j=b.length();i>=&&j>=;)
    {
        if(a[i-]==b[j-])
        {
            ans[w++]=a[i-];
            i--;
            j--;
        }
        else {
            if(dp[i][j-]>dp[i-][j])
            {
                j--;
            }
            else i--;
        }
    }
    for(j=w-;j>=;--j)
    cout<<ans[j];
    cout<<endl;
    return ;
}

（来源于51nod教程）。