mono-3.4.0 源码安装时出现的问题 [do-install] Error 2 [install-pcl-targets] Error 1 解决方法

Mono 3.4修复了很多bug，继续加强稳定性和性能（其实Mono 3.2.8 已经很稳定，性能也很好了），但是从http://download.mono-project.com/sources/mono/ 下载官方提供的源码安装Mono3.4 出现如下错误：

/usr/bin/install: cannot stat `targets/Microsoft.Portable.Common.targets': No such file or directory
make[7]: *** [install-pcl-targets] Error 1
make[7]: Leaving directory `/usr/local/files/mono-3.4.0/mcs/tools/xbuild'
make[6]: *** [do-install] Error 2
make[6]: Leaving directory `/usr/local/files/mono-3.4.0/mcs/tools/xbuild'
make[5]: *** [install-recursive] Error 1
make[5]: Leaving directory `/usr/local/files/mono-3.4.0/mcs/tools'
make[4]: *** [install-recursive] Error 1
make[4]: Leaving directory `/usr/local/files/mono-3.4.0/mcs'
make[3]: *** [profile-do--net_2_0--install] Error 2
make[3]: Leaving directory `/usr/local/files/mono-3.4.0/mcs'
make[2]: *** [profiles-do--install] Error 2
make[2]: Leaving directory `/usr/local/files/mono-3.4.0/mcs'
make[1]: *** [install-exec] Error 2
make[1]: Leaving directory `/usr/local/files/mono-3.4.0/runtime'
make: *** [install-recursive] Error 1

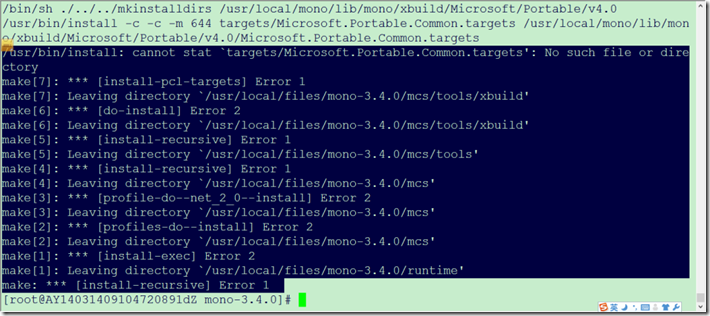
这是由于官方的mono源码包缺少个文件，所以会出错，可以下载我的云盘上共享的文件 http://pan.baidu.com/s/1eQ452Ie，参照这篇文章《CentOS 6.3下 安装 Mono 3.2 和Jexus 5.4》下载安装就没问题了。

附安装步骤：

1.系统环境 操作系统: CentOS 6.4 最小化安装

2.安装Mono

2.1安装libgdiplus

(1)安装缺失的组件 yum -y install wget glib2-devel libtiff libtiff-devel libjpeg libjpeg-devel giflib giflib-devel libpng libpng-devel libX11 libX11-devel freetype freetype-devel fontconfig fontconfig-devel libexif libexif-devel gcc-c++ gettext unzip zip

(2)下载 libgdiplus cd /usr/software wget http://download.mono-project.com/sources/libgdiplus/libgdiplus-2.10.tar.bz2 (3)安装 libgdiplus tar jvxf libgdiplus-2.10.tar.bz2 cd libgdiplus-2.10 ./configure --prefix=/usr make && make install

2.2安装Mono3.4.0

(1)下载 从百度网盘上下载最新的Mono, http://pan.baidu.com/s/1eQ452Ie 并上传到/usr/software目录 cd /usr/software
(2)安装 tar -xzf mono-3.4.0.tar.gz cd mono-3.4.0 ./configure --prefix=/usr make && make install 安装时间比较长,需要多等一会
3. 安装Jexus

(1)下载 cd /usr/software wget http://www.linuxdot.net/down/jexus-5.5.1.tar.gz 

(2)安装 tar -zxvf jexus-5.5.1.tar.gz  cd jexus-5.5.1  ./install

(3)测试是否安装成功 开启防火墙端口   启动Jexus服务器 /usr/jexus/jws start 在客户端浏览器中输入"服务器地址/info", 如"http://192.168.1.15/info",显示正常即表示安装成功

(4)基本使用 启动：sudo /usr/jexus/jws start 停止：sudo /usr/jexus/jws stop 重启：sudo /usr/jexus/jws restart 更多使用方法可在http://www.jexus.org/学习

欢迎各位热心Linux平台.NET应用程序开发，特别是希望基于Linux进行ASP.NET WEB网站建设的朋友，多多关注 http://www.linuxdot.net，或加入.NET LINUX QQ群：103810355。