duliu题之狼抓兔子题解

拖了将近5天的正解和AC.........emmmmm...........

事实告诉我们这种毒瘤题一定要建双向边（用了不知道多少个小时质疑建边的人欲哭无泪）

心态爆炸的传送

题了个面

这是个求最小割问题

说人话：

把图中的一些边砍断，使这个图分为不连通的两部分。砍断一条边的代价就是这条边的边权，求最小代价。

似乎是个定理的东西：

一个图的最小割是对偶图的最短路

question1:神马是对偶图？能吃吗？

当然不能

在这里的对偶图，就是把原来的块当做点，把原来的边建成与之垂直的边，边权不变，再在左下角和右上角新建两个点st,eend（这两个点放在哪个角上无所谓辣），作为源点和汇点，跑最短路。

为毛是eend而不是end呢？

因为在c++11下end会CE

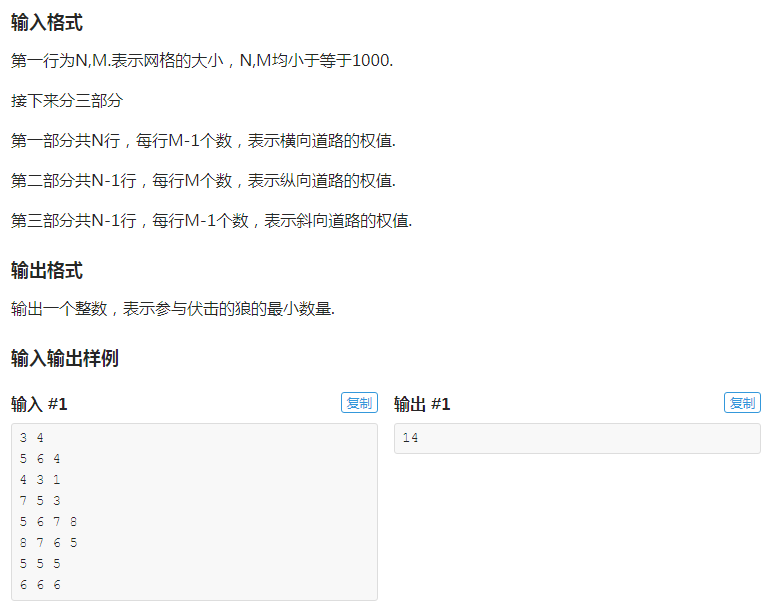
说的太抽象了，举个例子

原图：

对偶图：

思路很简单，but代码还是很难（它是个要面子的题）

我们想想怎么给这些点编号

（其实随便编号）

窝的编号方法：

接下来我们分边讨论怎么表示点（注意一定要建双向边）

横边：

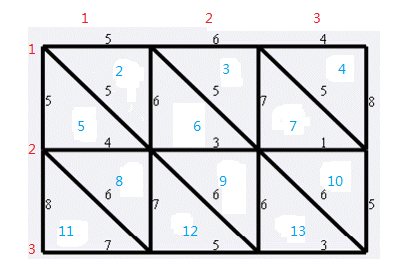
左边的红字是边的行号 i ,上边的是边的列号 j

我们要计算每条边(i,j)上面的点和下面的点，如果边的行号是1,则直接向终点eend建边，如果边的行号是 n ，就向起点st建边，否则，上下建边（注意建双向边*2）

点的表示方法：

上面的点 ss=2*(i-1)*(m-1)+j+1;

下面的点 ee=ss-m+1;

竖边：

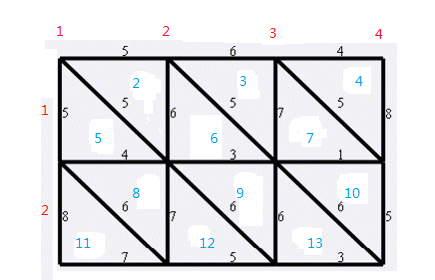
右边的点：ss=j+(m-1)*(2*(i-1)+1)+1;

左边的点：ee=ss-m;

当j=1时：st与右边的点连边

当j=m时：左边的点与eend连边

正常情况：左边的点与右边的点连边

注意建双向边！！！(*3)

斜边：

斜上方的点：ss=2*(i-1)*(m-1)+j+1;

斜下方的点：ee=ss+m-1;

这里就不需要考虑st和eend了

双向建边*5

建完边之后跑一遍dijkstra就好辣

Code:

#include<cstdio>
#include<cmath>
#include<cstring>
#include<queue>
#include<algorithm>
#define ll long long
#define pa pair<int,int>
using namespace std;
inline int read()
{
    char ch=getchar(),lst;
    int x=;
    while(ch<''||ch>'')
    {
        lst=ch;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        x=(x<<)+(x<<)+(ch^);
        ch=getchar();
    }return ((lst=='-')?-x:x);
}
int n,m,st=,eend,head[],cnt,dis[];
const int inf=;
bool vis[];
struct Ed{
    int to,nxt,dis;
}edge[];
void add(int fr,int to,int dis)
{
    cnt++;
    edge[cnt].to=to;
    edge[cnt].dis=dis;
    edge[cnt].nxt=head[fr];
    head[fr]=cnt;
}
void dij()//堆优化的dij
{
   for(int i=;i<=eend;i++)
    dis[i]=inf;
   dis[]=;
   priority_queue<pa,vector<pa>,greater<pa> > q;
   q.push(make_pair(,));
   while(!q.empty())
   {
    int now=q.top().second;
     q.pop();
     if(vis[now])continue;
     vis[now]=;
     for(int e=head[now];e;e=edge[e].nxt)
     {
        int v=edge[e].to,di=edge[e].dis;
        if(dis[now]+di<dis[v])
        {
            dis[v]=dis[now]+di;
            q.push(make_pair(dis[v],v));
        }
     }
   }
}
int main()
{
    n=read();m=read();
    eend=(n-)**(m-)+;
    for(int i=;i<=n;i++)//横边
    {
        for(int j=;j<=m-;j++)
        {
            int dis=read();
            int ss=*(i-)*(m-)+j+;
            int ee=ss-m+;
            if(i==)
                {add(ss,eend,dis);add(eend,ss,dis);
                continue;}
            if(i==n)
                {add(st,ee,dis);add(ee,st,dis);
                continue;}
            add(ss,ee,dis);add(ee,ss,dis);
        }
    }//竖边
    for(int i=;i<n;i++)
    {
        for(int j=;j<=m;j++)
        {
            int dis=read();
            int ss=j+(m-)*(*(i-)+)+;
            int ee=ss-m;
            if(j==)
            {add(st,ss,dis);add(ss,st,dis);
            continue;}
            if(j==m)
            {add(ee,eend,dis);add(eend,ee,dis);
            continue;}
            add(ee,ss,dis);add(ss,ee,dis);
        }
    }//斜边
    for(int i=;i<n;i++)
    {
        for(int j=;j<m;j++)
        {
            int dis=read();
            int ss=*(i-)*(m-)+j+;
            int ee=ss+m-;
            add(ee,ss,dis);
            add(ss,ee,dis);
        }
    }
    dij();
    printf("%d",dis[eend]);
}