「FJOI2018」领导集团问题 解题报告

「FJOI2018」领导集团问题

题意：给你一颗\(n\)个点的带点权有根树，选择一个点集\(S\)，使得点集中所有祖先的点权$\le \(子孙的点权，最大化\)|S|$（出题人语死早...）

---

• 一个显然的\(dp\)

  \(dp_{i,j}\)代表子树\(i\)中选择的点集中最小的点权为\(j\)时的最大值。

• 一个朴素的转移需要维护一个后缀最大值

  设为\(f_{i,j}=\max\limits_{k\ge i} dp_{i,k}\)

• 一些显然的事实

  • 后缀最大值中仅有最多\(siz_v\)（指子树大小）个权值不同的位置
  • 后缀最大值单调不增

于是我们考虑如何合并两颗子树有限的后缀最大值

在不考虑关键点时，我们只需要对应位置两两加和就可以了，即

\[dp_{i,j}=\sum_vf_{v,j}
\]

下面我们仅考虑关键点

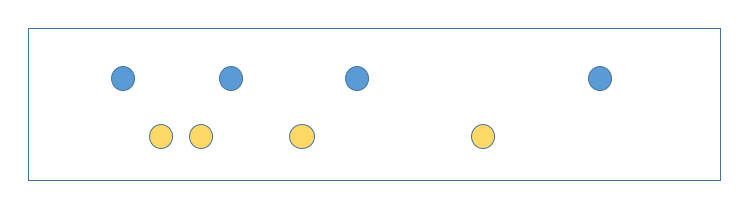
如图所示，蓝色的关键点是子树\(u\)的关键点，黄色的是子树\(v\)的关键点，注意到关键点是左边位置的值与它相等。

考虑启发式合并，但是我们注意到关键点是互相影响的，就是黄影响蓝，蓝影响黄。

其实这样可以做，但是比较麻烦。

注意到一个事实，我们只需要求\(f_{rt,0}\)，所以我们考虑维护后缀最大值\(f\)的差分数组。

这样我们合并两个关键点集合，直接对关键点进行相加就可以了，考虑直接用线段树合并维护。

然后我们还需要计算根\(i\)自己的贡献，设\(i\)的权值为\(w_i\)

考虑到根直接的贡献是使\(dp_{i,w_i}=f_{i,w_i}+1\)

然后从这个\(w_i\)往左边走，找到第一个\(f_{i,p}\)比\(f_{i,w_i}\)大\(1\)的位置，然后更新这一段的贡献，就是一个区间加。具体操作就是在\(p\)打个\(-1\)，在\(w_i\)打一个\(1\)

形象一点就是把这一段铺平了,就是那\(dp\)再回去贡献\(f\)

找第一个位置就是在差分意义下就是找一个非\(0\)位置，可以在线段树上进行二分操作找到。

---

Code:

#include <cstdio>
#include <cctype>
#include <vector>
#include <algorithm>
using std::min;
using std::max;
const int SIZE=1<<21;
char ibuf[SIZE],*iS,*iT;
//#define gc() (iS==iT?(iT=(iS=ibuf)+fread(ibuf,1,SIZE,stdin),iS==iT?EOF:*iS++):*iS++)
#define gc() getchar()
template <class T>
void read(T &x)
{
	int f=0;x=0;char c=gc();
	while(!isdigit(c)) f|=c=='-',c=gc();
	while(isdigit(c)) x=x*10+c-'0',c=gc();
	if(f) x=-x;
}
const int N=4e5+10;
int n,m,w[N],yuy[N];
int head[N],to[N],Next[N],cnt;
void add(int u,int v)
{
	to[++cnt]=v,Next[cnt]=head[u],head[u]=cnt;
}
int root[N],ch[N*40][2],sum[N*40],tot;
#define ls ch[now][0]
#define rs ch[now][1]
void upt(int &now,int l,int r,int p,int d)
{
	if(!now) now=++tot;
	if(l==r)
	{
		sum[now]+=d;
		return;
	}
	int mid=l+r>>1;
	if(p<=mid) upt(ls,l,mid,p,d);
	else upt(rs,mid+1,r,p,d);
	sum[now]=sum[ls]+sum[rs];
}
int qry(int now,int l,int r,int p)
{
	if(!now||!p) return 0;
	if(l==r) return sum[now]?l:0;
	int mid=l+r>>1;
	if(p<=mid) return qry(ls,l,mid,p);
	else
	{
		int ret=qry(rs,mid+1,r,p);
		if(ret) return ret;
		else return qry(ls,l,mid,p);
	}
}
int Merge(int x,int y,int l,int r)
{
	if(!x||!y) return x^y;
	if(l==r)
	{
		sum[x]+=sum[y];
		return x;
	}
	int mid=l+r>>1;
	ch[x][0]=Merge(ch[x][0],ch[y][0],l,mid);
	ch[x][1]=Merge(ch[x][1],ch[y][1],mid+1,r);
	sum[x]=sum[ch[x][0]]+sum[ch[x][1]];
	return x;
}
void dfs(int now)
{
	for(int v,i=head[now];i;i=Next[i])
	{
		dfs(v=to[i]);
		root[now]=Merge(root[now],root[v],0,m);
	}
	upt(root[now],1,m,w[now],1);
	int pos=qry(root[now],1,m,w[now]-1);
	if(pos) upt(root[now],1,m,pos,-1);
}
int main()
{
	read(n);
	for(int i=1;i<=n;i++) read(w[i]),yuy[i]=w[i];
	std::sort(yuy+1,yuy+1+n);
	m=std::unique(yuy+1,yuy+1+n)-yuy-1;
	for(int i=1;i<=n;i++) w[i]=std::lower_bound(yuy+1,yuy+1+m,w[i])-yuy;
	for(int p,i=2;i<=n;i++) read(p),add(p,i);
	dfs(1);
	printf("%d\n",sum[root[1]]);
	return 0;
}

---

2019.5.21