探究"补阶乘大法的本质"——糖水不等式！

废话不多说先来康一条例题：

　　证明: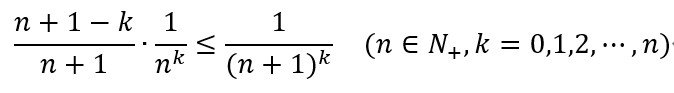

下面给出题目的一种解法（我称之为"补阶乘大法"）：

思考：为什么补上一个阶乘（准确说不是阶乘，是两个数阶乘的之商）项，放缩后再给去掉，就能达到我们的目的呢？

要探究其中的奥秘，不妨看一看放缩的细节：

整个放缩就是k-1个这样的小放缩相乘而得，我们稍微变形一下，得到：

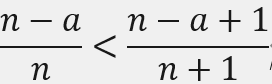
熟悉吧，这就是著名的糖水不等式。

我们试试将k个糖水不等式相乘，得到如下不等式：

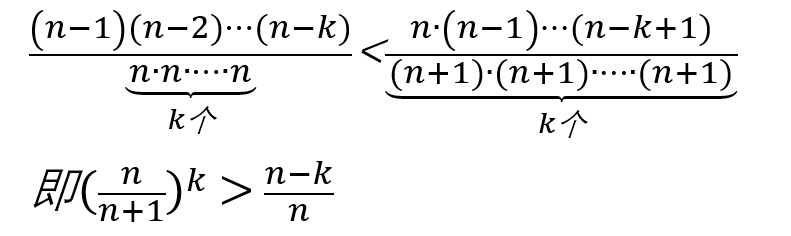
累乘后，分子部分可以消去很多项，最后留下一个指数式和分式的不等关系。（细品这个不等式真的挺妙的。。）

诶，是不是发现放缩比例题那个放多了？没事，我们用k-1代k稍微变形一下：

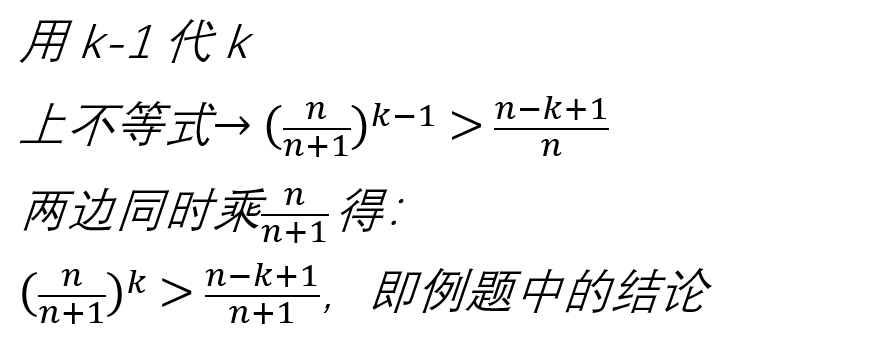
所以我们发现，代入k里的值越小，放缩程度越小。其实也很好理解，k越小，同时相乘的小不等式越少，放缩的程度当然也相应减小。

在这里，糖水不等式发挥了重要的作用。

看似很简单的不等式，当他们累乘起来后，却搭建起了指数式和分数式的不等关系的桥梁。