Catalan 数

概要

在一些面试的智力题中会遇到此数的变形，如果完全不了解，直接想结果是很困难的，故在此简单介绍一下。

 

---

基本定义

Catalan 数的定义根据不同的应用环境有很多不同的定义方式，下面给出一个。

  Catalan 数：一个凸 \(n\) 边形，通过不相交于 \(n\) 边形内部的对角线，把 \(n\) 边形拆分成若干三角形，不同拆分的数目用 \(f(n)\) 表示，即称为 Catalan 数.

例如下五边形： 有 \(f(5) = 5\).

它有以下的递推关系：
\begin{align} \label{e1}
f(n+1) &= f(2)f(n)+f(3)f(n-1)+\cdots+f(n)f(2) = \sum_{k=2}^nf(k)f(n-k+2),\qquad f(2) = f(3) = 1 \\ \label{e2}
(n-3)f(n)&= \frac{n}{2}(f(3)f(n-1)+f(4)f(n-2)+\cdots+f(n-2)f(4)+f(n-1)f(3))
\end{align}

  证明：(a) 如下图：

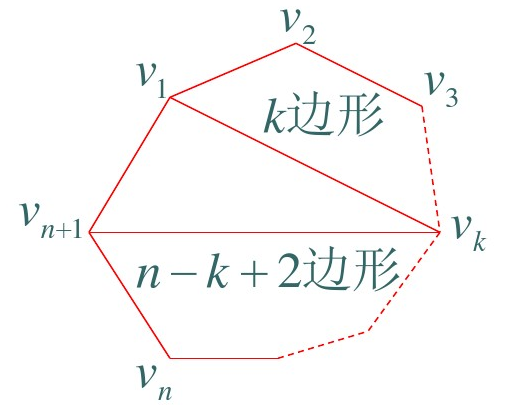
以 \(v_1v_{n+1}\) 作为一个边的三角形 \(v_1v_kv_{n+1}\)，将凸 \(n+1\) 边形分割成两部分，一部分是 \(k\) 边形，一部分是 \(n-k+2\) 边形，\(k=2,3,\cdots,n\). 依据加法法则有 \(f(n+1) = \sum_{k=2}^nf(k)f(n-k+2)\).

(b) 如下图：

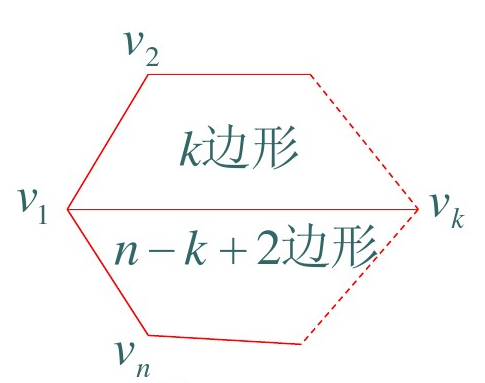
从 \(v_1\) 点向其它 \(n-3\) 个顶点 \(\{v_3,v_4,\cdots,v_{n-1}\}\) 可引出 \(n-3\) 条对角线。对角线 \(v_1v_k\) 把 \(n\) 边形分割成两个部分，因此以 \(v_1v_k\) 对角线作为拆分线的方案数为 \(f(k)f(n-k+2)\)，\(v_k\) 可以是 \(\{v_3,v_4,\cdots,v_{n-1}\}\) 中任一点，对所有这些点求和得：\(f(3)f(n-1)+f(4)f(n-2)+\cdots+f(n-2)f(4)+f(n-1)f(3)\). 以 \(v_2,v_3,\cdots,v_n\) 取代 \(v_1\) 点也有类似的结果。但考虑到对角线有两个顶点，同一对角线在两个顶点分别计算了一次，下式
\begin{align}
\frac{n}{2}(f(3)f(n-1)+f(4)f(n-2)+\cdots+f(n-2)f(4)+f(n-1)f(3))
\end{align}
没有给出剖分数，无疑其中有重复的。其重复度是由于一个凸边形的部分有 \(n-3\) 条对角线，而对其每一条边计数时该剖分都计数了一次，故重复了 \(n-3\) 次，即该式给出的结果是 \(f(n)\) 的 \(n-3\) 倍，证毕。

我们有了递推关系，下面说一下其计算公式。由式 \ref{e1} 及 \(f(2)=1\) 知：
\begin{align}
f(n+1)-2f(n) = f(3)f(n-1)+f(4)f(n-2)+\cdots+f(n-2)f(4)+f(n-1)f(3)
\end{align}
结合式 \ref{e2} 知
\begin{align}
(n-3)f(n) = \frac{n}{2}(f(3)f(n-1)+f(4)f(n-2)+\cdots+f(n-2)f(4)+f(n-1)f(3)) = \frac{n}{2} (f(n+1)-2f(n) )
\end{align}
整理得：
\begin{align}
nf(n+1) = (4n-6)f(n)
\end{align}
令 \(g(n+1) = nf(n+1)\) 得
\begin{align}
g(n+1) = (4n-6) \frac{g(n)}{n-1} = \frac{(2n-2)(2n-3)}{(n-1)(n-1)}g(n), \quad g(2) = f(2) = 1
\end{align}
则有以下等式成立：
\begin{align}
g(n+1) &= \frac{g(n+1)}{g(n)} \cdot \frac{g(n)}{g(n-1)} \cdot \frac{g(n-1)}{g(n-2)} \cdots \frac{g(4)}{g(3)} \cdot \frac{g(3)}{g(2)} \notag \\
&=\frac{(2n-2)(2n-3)}{(n-1)(n-1)} \cdot \frac{(2n-4)(2n-5)}{(n-2)(n-2)} \cdots \frac{(4)(3)}{(2)(2)} \cdot \frac{(2)(1)}{(1)(1)} \notag \\
&= \frac{(2n-2)!}{(n-1)!(n-1)!} = C_{2n-2}^{n-1} = nf(n+1) \notag
\end{align}
所以有最终的计算公式：
\begin{align}
f(n+1) = \frac{1}{n} C_{2n-2}^{n-1}
\end{align}
 

应用举例

 
  例 1. \(n\) 个 \(1\) 和 \(n\) 个 \(0\) 组成一 \(2n\) 位的二进制数，要求从左到右扫描，\(1\) 的累计数不小于 \(0\) 的累计数，试求满足这条件的数有多少？（与网易 2018 春季数据分析实习生笔试类似）

  解： 设 \(p_{2n}\) 为所求结果。在 \(2n\) 位上填入 \(n\) 个 \(1\) 的方案为 \(C_{2n}^n\)，不填 \(1\) 的其余 \(n\) 位自动填以数 \(0\)。从 \(C_{2n}^n\) 中减去不符合要求的方案即为所求。

不合要求的数指的是从左而右扫描，出现 \(0\) 的累计数超过 \(1\) 的累计数的数。不合要求的数的特征是从左到右扫描时，必然，在某一奇数 \(2m+1\) 位上首先出现 \(m+1\) 个 \(0\) 的累计数，和 \(m\) 个 \(1\) 的累计数。此后的 \(2(n-m)-1\) 位上有 \(n-m\) 个 \(1\)，\(n-m-1\) 个 \(0\). 如若把后面这部分 \(2(n-m)-1\) 位，\(0\) 与 \(1\) 交换，使之成为 \(n-m\) 个 \(0\)，\(n-m-1\) 个 \(1\)，结果得一个由 \(n+1\) 个 \(0\) 和 \(n-1\) 个 \(1\) 组成的 \(2n\) 位数，即一个不合要求对应于一个由 \(n-1\) 个 \(0\) 和 \(n+1\) 个 \(1\) 组成的一个排列。反过来，任何一个由 \(n+1\) 个 \(0\)，\(n-1\) 个 \(1\) 组成的 \(2n\) 位数，由于 \(0\) 的个数多两个，\(2n\) 是偶数，故必在某一个奇数位上出现 \(0\) 的累计数超过 \(1\) 的累计数。同样在后面部分，令 \(0\) 和 \(1\) 互换，使之成为由 \(n\) 个 \(0\) 和 \(n\) 个 \(1\) 组成的 \(2n\) 位数。即 \(n-1\) 个 \(0\) 和 \(n+1\) 个 \(1\) 组成的 \(2n\) 位数，必对应于一个为合要求的数。

上述方法建立了由 \(n+1\) 个 \(0\) 和 \(n-1\) 个 \(1\) 组成的 \(2n\) 位数，与由 \(n\) 个 \(0\) 和 \(n\) 个 \(1\) 组成的 \(2n\) 位数中从左向右扫描出现 \(0\) 的累计数超过 \(1\) 的累计数的数一一对应。因而不合要求的 \(2n\) 位数与 \(n+1\) 个 \(0\)，\(n-1\) 个 \(1\) 组成的排列一一对应 ，故有

\begin{align}
p_{2n} = C_{2n}^n - C_{2n}^{n+1} = (2n)! \left[ \frac{1}{n!n!} -\frac{1}{(n-1)!(n+1)!}\right] = \frac{(2n)!}{(n+1)!n!} = \frac{1}{n+1}C_{2n}^n = f(n+2)
\end{align}

上个问题对应下图左中从原点 \((0,0)\) 到 \((n,n)\) 点的路径要求中途所经过的点 \((a,b)\) 满足关系 \(a\leqslant b\).

对应的办法是从 \((0,0)\) 出发，对 \(2n\) 位数从左而右扫描，若遇到 \(1\) 便沿 \(y\) 轴正方向走一格；若遇到 \(0\) 便沿 \(x\) 轴正方向走一格。由于有 \(n\) 个 \(0\)，\(n\) 个 \(1\)，故对应一条从 \((0,0)\) 点到 \((n,n)\) 点的路径。由于要求 \(1\) 的累计数不少于 \(0\) 的累计数，故可以途经对角线 \(OA\) 上的点，但不允许穿越过对角线。反过来，满足这条件的路径对应一满足要求的 \(2n\) 位二进制数。

 
  例 2. 将例 1 中的 \(1\) 看成左括号，\(0\) 看成右括号，就变成了合法括号表达式的个数。比如两个左括号和两个右括号组成的合法表达式有 \(p_4 = f(2+2) = 2\) 种，即 \(()()\) 和 \((())\).
 
  例 3. \(n\) 个数入栈后出栈的排列总数是 \(f(n+2)\). 比如 \(1,2,3\) 的出栈顺序有 \(123,132,213,231,321\) 五种。