FFT快速傅里叶变换算法

1、FFT算法概要：

FFT（Fast Fourier Transformation）是离散傅氏变换（DFT）的快速算法。即为快速傅氏变换。它是根据离散傅氏变换的奇、偶、虚、实等特性，对离散傅立叶变换的算法进行改进获得的。

2、FFT算法原理：

离散傅里叶变换DFT公式：

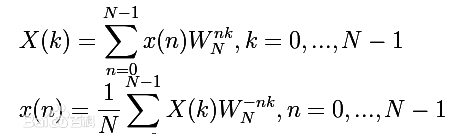
FFT算法(Butterfly算法)

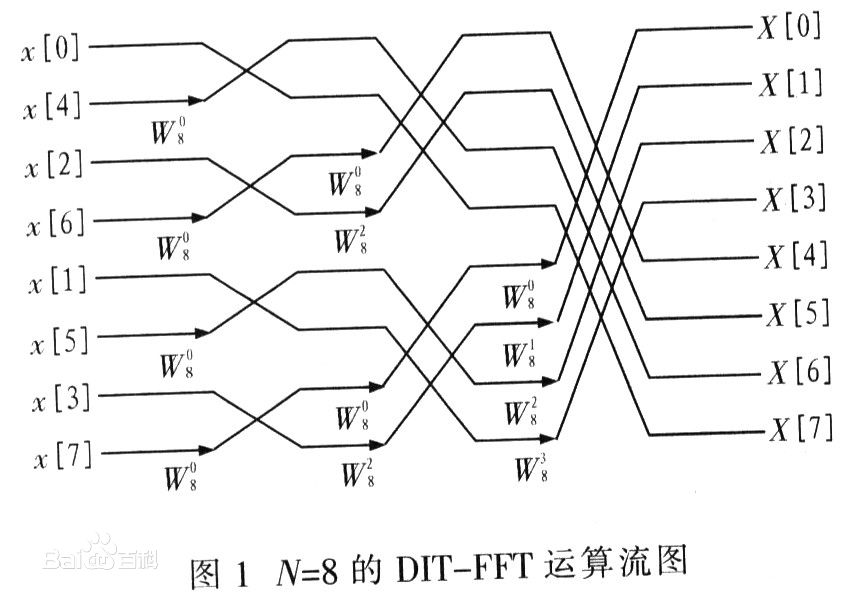
设x(n)为N项的复数序列，由DFT变换，任一X（m）的计算都需要N次复数乘法和N-1次复数加法，而一次复数乘法等于四次实数乘法和两次实数加法，一次复数加法等于两次实数加法，即使把一次复数乘法和一次复数加法定义成一次“运算”（四次实数乘法和四次实数加法），那么求出N项复数序列的X（m）,即N点DFT变换大约就需要N^2次运算。当N=1024点甚至更多的时候，需要N2=1048576次运算，在FFT中，利用WN的周期性和对称性，把一个N项序列（设N=2k,k为正整数），分为两个N/2项的子序列，每个N/2点DFT变换需要（N/2）2次运算，再用N次运算把两个N/2点的DFT变换组合成一个N点的DFT变换。这样变换以后，总的运算次数就变成N+2*（N/2)^2=N+（N^2）/2。继续上面的例子，N=1024时，总的运算次数就变成了525312次，节省了大约50%的运算量。而如果我们将这种“一分为二”的思想不断进行下去，直到分成两两一组的DFT运算单元，那么N点的DFT变换就只需要N/2log2N次的运算，N在1024点时，运算量仅有5120次，是先前的直接算法的近1/200，点数越多，运算量的节约就越大，这就是FFT的优越性。

3、FFT算法官方实现：

       

搭建FFTW库并生成所需要的lib文件：

Step1：从官网下载对应的.zip文件，例如我是win10_x86的操作系统，下载64bit的安装包：

Step2：下载完成之后解压到你希望安装的FFTW库的位置

Step3：打开CMD命令操作行，切换到Step2中的安装目录下，执行下面的指令代码生成.lib文件(需要安装Visual Studio，用VC++中的lib命令生成系统能够使用的.lib文件)

打开的方式为，按下window键，输入vs，小娜会自动帮你查找对应的File。

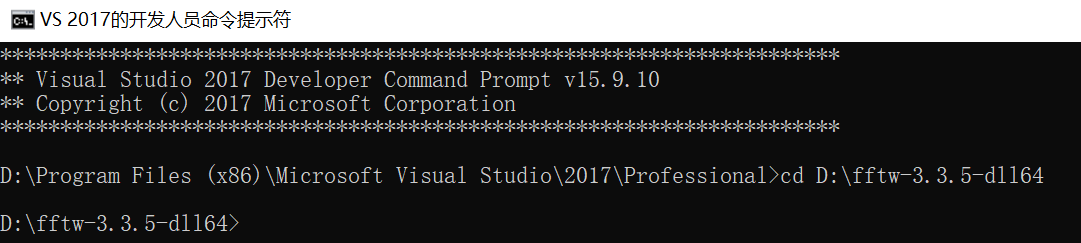切换到对应的路径之后就可以使用lib命令来生成.lib文件了：

 lib /def:libfftw3-.def
 lib /def:libfftw3f-.def
 lib /def:libfftw3l-.def

查看对应的目录，我们就能看到生成的.lib文件：

在工程中使用FFTW库

首先在VS2017中创建一个工程命名为FFTW_Test

FFTW_Test.cpp文件内容如下：

 #include <stdio.h>
 #include <iostream>

 #include "fftw3.h"
 #pragma comment(lib, "libfftw3-3.lib")

 using namespace std;

 int main(void)
 {
     /*
     *fftw_complex 是FFTW自定义的复数类
     *引入<complex>则会使用STL的复数类
     */
     fftw_complex x[];
     fftw_complex y[];

     for (int i = ; i < ; i++) {
         x[i][REAL] = i;
         x[i][IMAG] = ;
     }

     //定义plan，包含序列长度、输入序列、输出序列、变换方向、变换模式
     fftw_plan plan = fftw_plan_dft_1d(, x, y, FFTW_FORWARD, FFTW_ESTIMATE);

     //对于每个plan，应当"一次定义 多次使用"，同一plan的运算速度极快
     fftw_execute(plan);

     for (int i = ; i < ; i++) {
         cout << y[i][REAL] << "  " << y[i][IMAG] << endl;
     }

     //销毁plan
     fftw_destroy_plan(plan);
 }

将FFTW相关的库文件拷贝到FFTW_Test工程目录下，拷贝的位置需要和FFTW_Test.cpp在同一个目录当中！

拷贝的文件如下图所示(只需要将FFTW安装目录下的这三个文件拷贝过去即可)：

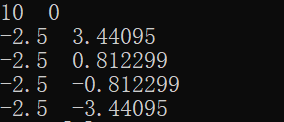
程序运行结果：

参考资料

• 官方网址：http://www.fftw.org/
• 官方下载：http://www.fftw.org/download.html
• 其他参考：https://blog.csdn.net/cyh706510441/article/details/46676123

4、FFT算法C/C++/Python代码：

Code1(DFT)：

 char DFT_Alg(float *Signal, float *Fre, int L)
 {
     long long i,j;
     float real, imag, coff1, coff2;
     coff1 = -*pi/L;
     for(i=;i<L;i++){
         for(j=;j<L;j++){
             coff2 = coff1*i*j;
             real += Signal[j]*cos(coff2);
             imag += Signal[j]*sin(coff2);
         }
         printf("Processing:%d\n",i);
         Fre[i] = real*real + imag*imag;
     }
     return ;
 }

Code2(FFT)：

 typedef float FFT_TYPE;

 #ifndef PI
     #define PI (3.14159265f)
 #endif

 typedef struct complex_st {
     FFT_TYPE real;
     FFT_TYPE img;
 } complex;

 static void BitReverse(complex *x, complex *r, int n, int l)
 {
     int i = ;
     int j = ;
     short stk = ;
     static complex *temp = ;

     temp = (complex *)malloc(sizeof(complex) * n);
     if (!temp) {
         return;
     }

     for(i=; i<n; i++) {
         stk = ;
         j = ;
         do {
             stk |= (i>>(j++)) & 0x01;
             if(j<l)
             {
                 stk <<= ;
             }
         }while(j<l);

         if(stk < n) {             /* 满足倒位序输出 */
             temp[stk] = x[i];
         }
     }
     /* copy @temp to @r */
     for (i=; i<n; i++) {
         r[i] = temp[i];
     }
     free(temp);
 }

 int fft(complex *x, int N)
 {
     int i,j,l,ip;
     static int M = ;
     static int le,le2;
     static FFT_TYPE sR,sI,tR,tI,uR,uI;

     M = (int)(log(N) / log());

     BitReverse(x,x,N,M);

     for (l=; l<=M; l++) {
         le = (int)pow(,l);
         le2 = (int)(le / );
         uR = ;
         uI = ;
         sR = cos(PI / le2);
         sI = -sin(PI / le2);
         for (j=; j<=le2; j++) {
             //jm1 = j - 1;
             for (i=j-; i<=N-; i+=le) {
                 ip = i + le2;
                 tR = x[ip].real * uR - x[ip].img * uI;
                 tI = x[ip].real * uI + x[ip].img * uR;
                 x[ip].real = x[i].real - tR;
                 x[ip].img = x[i].img - tI;
                 x[i].real += tR;
                 x[i].img += tI;
             }
             tR = uR;
             uR = tR * sR - uI * sI;
             uI = tR * sI + uI *sR;
         }
     }
     return ;
 }
 int ifft(complex *x, int N)
 {
     int k = ;
     for (k=; k<=N-; k++) {
         x[k].img = -x[k].img;
     }
     fft(x, N);    /* using FFT */
     for (k=; k<=N-; k++) {
         x[k].real = x[k].real / N;
         x[k].img = -x[k].img / N;
     }
     return ;
 }

Code3(DFT-Python)：

 def DFT(x):
     """
     Input:
         x (numpy array) = input sequence of length N
     Output:
         The function should return a numpy array of length N
         X (numpy array) = The N point DFT of the input sequence x
     """
     N = len(x)
     real = np.zeros(N)
     imag = np.zeros(N)
     for i in range(N):
         for j in range(N):
             real[i] += x[j]*np.cos(-2*np.pi*i*j/N)
             imag[i] += x[j]*np.sin(-2*np.pi*i*j/N)
     Res = 1j*imag + real
     return Res
 def IDFT(X):
     """
     Input:
         X (numpy array) = frequency spectrum (length N)
     Output:
         The function should return a numpy array of length N
         x (numpy array) = The N point IDFT of the frequency spectrum X
     """
     N = len(X)
     real = np.zeros(N)
     imag = np.zeros(N)
     for i in range(N):
         for k in range(N):
             param1 = X[k].real
             param2 = X[k].imag
             sin = np.sin(2*np.pi*i*k/N)
             cos = np.cos(2*np.pi*i*k/N)
             real[i] += param1*cos-param2*sin
             imag[i] += param1*sin+param2*cos
     Res = 1j*imag/N + real/N
     return Res

5、多种平台的FFT算法移植：

未完待续