Loj #2321. 「清华集训 2017」无限之环

Loj #2321. 「清华集训 2017」无限之环

曾经有一款流行的游戏，叫做 *Infinity Loop***，先来简单的介绍一下这个游戏:

游戏在一个 \(n \times m\) 的网格状棋盘上进行，其中有些小方格中会有水管，水管可能在方格某些方向的边界的中点有接口，所有水管的粗细都相同，所以如果两个相邻方格的公共边界的中点都有接头，那么可以看作这两个接头互相连接。水管有以下 \(15\) 种形状：

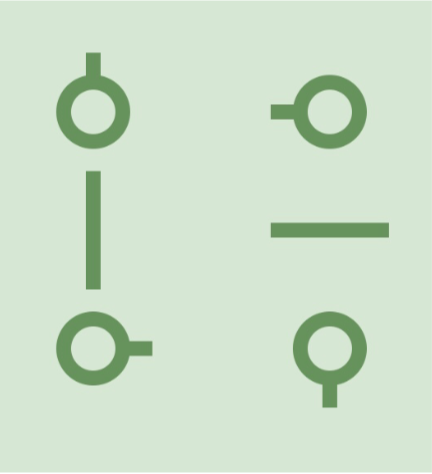
游戏开始时，棋盘中水管可能存在漏水的地方。

形式化地:如果存在某个接头，没有和其它接头相连接，那么它就是一个漏水的地方。

玩家可以进行一种操作：选定一个含有*非直线型*水管的方格，将其中的水管绕方格中心顺时针或逆时针旋转 \(90\) 度。

直线型水管是指左图里中间一行的两种水管。

现给出一个初始局面，请问最少进行多少次操作可以使棋盘上不存在漏水的地方。

输入格式

第一行两个正整数 \(n,m\)，代表网格的大小。

接下来 \(n\) 行每行 \(m\) 个数，每个数是 \([0,15]\) 中的一个，你可以将其看作一个 \(4\) 位的二进制数，从低到高每一位分别代表初始局面中这个格子上、右、

下、左方向上是否有 水管接头。

特别地，如果这个数是 \(0\)，则意味着这个位置没有水管。

比如 \(3(0011_{(2)})\) 代表上和右有接头，也就是一个 L 型，而 \(12(1100_{(2)})\) 代表下和左有接头，也就是将 L 型旋转 \(180\) 度。

输出格式

输出共一行，表示最少操作次数。如果无法达成目标，输出 \(-1\).

数据范围与提示

\(n \times m \le 2000\)

orz

好神仙啊!

大致思路就是用一个水管的旋转代替所有水管的旋转。

代码：

#include<bits/stdc++.h>
#define ll long long
#define N 10005
using namespace std;
inline int Get() {int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();}while('0'<=ch&&ch<='9') {x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}return x*f;}
int n,m;
struct road {
	int to,next;
	int flow,cost;
}s[N*200];
int h[N],cnt=1;
void add(int i,int j,int f,int c) {
	s[++cnt]=(road) {j,h[i],f,c};h[i]=cnt;
	s[++cnt]=(road) {i,h[j],0,-c};h[j]=cnt;
}
int S,T;
int dis[N];
queue<int>q;
int e[N],fr[N];
bool in[N];
int ans,maxflow;
bool spfa() {
	memset(dis,0x3f,sizeof(dis));
	dis[S]=0;
	q.push(S);
	while(!q.empty()) {
		int v=q.front();
		q.pop();
		in[v]=0;
		for(int i=h[v];i;i=s[i].next) {
			int to=s[i].to;
			if(s[i].flow&&dis[to]>dis[v]+s[i].cost) {
				dis[to]=dis[v]+s[i].cost;
				fr[to]=v;
				e[to]=i;
				if(!in[to]) in[to]=1,q.push(to);
			}
		}
	}
	if(dis[T]>1e9) return 0;
	for(int i=T;i!=S;i=fr[i]) {
		s[e[i]].flow--;
		s[e[i]^1].flow++;
	}
	maxflow++;
	ans+=dis[T];
	return 1;
}
vector<int>pipe;
int tot;
int ID[2005][2005][5];
int dx[]={-1,0,1,0},dy[]={0,1,0,-1};
int mp[2005][2005];
int main() {
	n=Get(),m=Get();
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			mp[i][j]=Get();
	T=n*m+1;
	tot=T;
	int lpipe=0,rpipe=0;
	for(int i=1;i<=n;i++) {
		for(int j=1;j<=m;j++) {
			int id=(i-1)*m+j;
			int a=mp[i][j];
			pipe.clear();
			for(int k=0;k<4;k++) if(a>>k&1) pipe.push_back(k);
			for(int k=0;k<4;k++) ID[i][j][k]=++tot;
			if(i+j&1) {
				lpipe+=pipe.size();
				add(S,id,pipe.size(),0);
				for(int k=0;k<pipe.size();k++) add(id,ID[i][j][pipe[k]],1,0);
				if(a==10||a==5||a==15) continue ;
				if(pipe.size()==1) {
					int now=pipe[0];
					add(ID[i][j][now],ID[i][j][(now+1)%4],1,1);
					add(ID[i][j][now],ID[i][j][(now+2)%4],1,2);
					add(ID[i][j][now],ID[i][j][(now+3)%4],1,1);
				} else if(pipe.size()==2) {
					for(int k=0;k<pipe.size();k++) {
						int now=pipe[k];
						add(ID[i][j][now],ID[i][j][(now+2)%4],1,1);
					}
				} else if(pipe.size()==3) {
					int now;
					for(int k=0;k<4;k++) if(!(a>>k&1)) now=k;
					for(int k=0;k<3;k++) {
						if((pipe[k]+2)%4==now) add(ID[i][j][pipe[k]],ID[i][j][now],1,2);
						else add(ID[i][j][pipe[k]],ID[i][j][now],1,1);
					}
				}
			} else {
				rpipe+=pipe.size();
				add(id,T,pipe.size(),0);
				for(int k=0;k<pipe.size();k++) add(ID[i][j][pipe[k]],id,1,0);
				if(a==10||a==5||a==15) continue ;
				if(pipe.size()==1) {
					int now=pipe[0];
					add(ID[i][j][(now+1)%4],ID[i][j][now],1,1);
					add(ID[i][j][(now+2)%4],ID[i][j][now],1,2);
					add(ID[i][j][(now+3)%4],ID[i][j][now],1,1);
				} else if(pipe.size()==2) {
					for(int k=0;k<pipe.size();k++) {
						int now=pipe[k];
						add(ID[i][j][(now+2)%4],ID[i][j][now],1,1);
					}
				} else if(pipe.size()==3) {
					int now;
					for(int k=0;k<4;k++) if(!(a>>k&1)) now=k;
					for(int k=0;k<3;k++) {
						if((pipe[k]+2)%4==now) add(ID[i][j][now],ID[i][j][pipe[k]],1,2);
						else add(ID[i][j][now],ID[i][j][pipe[k]],1,1);
					}
				}
			}
		}
	}
	for(int i=1;i<=n;i++) {
		for(int j=1;j<=m;j++) {
			if(i+j&1) {
				for(int d=0;d<4;d++) {
					int X=i+dx[d],Y=j+dy[d];
					if(1<=X&&X<=n&&1<=Y&&Y<=m) {
						add(ID[i][j][d],ID[X][Y][(d+2)%4],1,0);
					}
				}
			}
		}
	}
	if(lpipe!=rpipe) cout<<-1;
	else {
		while(spfa());
		if(maxflow!=lpipe) cout<<-1;
		else cout<<ans;
	}
	return 0;
}