DP：0-1背包问题

【问题描述】

0-1背包问题：有 N 个物品，物品 i 的重量为整数 wi >=0，价值为整数 vi >=0，背包所能承受的最大重量为整数 C。如果限定每种物品只能选择0个或1个，求可装的最大价值。

可以用公式表示为：

 【算法思路】

动态规划法。我们可以想到这个问题具有最优子结构性质，假设（x1，x2，...，xn）是最优解，那么在去除x1之后，剩下（x2，...，xn）肯定是以下问题的最优解：

根据这个特征可以设计DP函数并推出递归关系。具体地，m(i，j)是背包容量为j，可选择物品为i，i+1，…，n时0-1背包问题的最优值。由0-1背包问题的最优子结构性质，则:

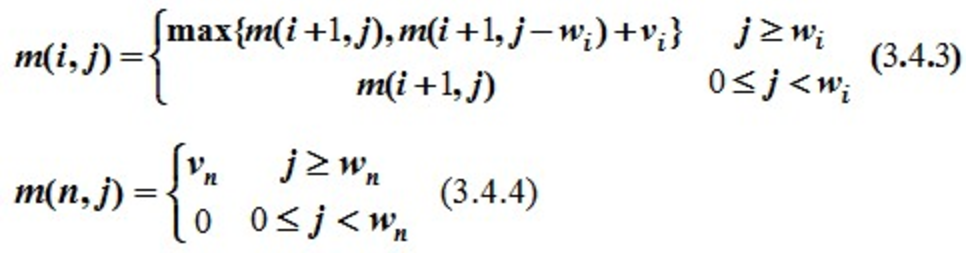
按着DP[N][C]的矩阵一个一个从 下 往 上 填就可以了，最后的结果是 DP(1,C)。要输出选取的样本编号的时候可以从前往后， DP(1,C)== DP(2,C)，则x1=0，否则1，依次类推即可。

【代码】

 #include<iostream>
 #include<algorithm>
 #include <stdio.h>
 #define MAXN 10000
 using namespace std;

 int W[MAXN];
 int V[MAXN];
 int DP[MAXN][MAXN]= {};

 int knapsack(int C, int N, int W[], int V[], int DP[][MAXN])
 {
     int lackL = min(C, W[N]-);
     for(int j = ; j <=lackL; j++) DP[N][j] = ;
     for(int j = W[N]; j <=C; j++) DP[N][j] = V[N];
     for(int i = N - ; i>=; i--){
         lackL = min(C, W[i]-);
         for(int j = ; j <=lackL; j++) DP[i][j] = DP[i+][j];
         for(int j = W[i]; j <=C; j++){
             DP[i][j] = max( DP[i+][j], DP[i+][j-W[i]] + V[i] );
         }
     }
     return DP[][C];
 }

 int main()
 {
     int C, N;
     cin >> C >> N;
     for(int i = ; i <=N; i++) {
         cin >> W[i] >> V[i];
     }
     cout<<knapsack(C, N, W, V, DP)<<endl;

     return ;
 }

【拓展】

如果现在的物品重量weight和背包容量C都是正整数，那么当他们是实数时，如何改进算法满足问题呢？

待完善（算法设计与分析P73）