[noip模拟]种花<快速幂+结论>

描述：

OI太可怕了，我决定回家种田。
我在后院里开辟了一块圆形的花圃，准备种花。种花是一种艺术，通过一定技术手法，花材的排列组合会让花变得更加的赏心悦目，这就是花艺。
当然你知道，我在种田之前是OIer，所以我不懂花艺，只会排列组合。我把花圃从圆心向外画线，分成了N块扇形，分别编号为1，2，3.....N，再从村里的商店采购了M种花。然后我大胆的决定：花圃中的每块只种M种花中的一种，相邻的两块不能种同一种花。我反应比较慢，所以我请来了机房里手速最快的强袭黯灭勋章鱼人守卫来帮我，让他试一下每种排列，看看哪种最令人赏心悦目。
有一些人，他们的美丽就在身边，也许就在自己身上，像艺术家一样，他们的眼光独到特别，可就因为他们不是艺术家，他们不被人们认可，被称之为另类。简单真实的事情总可以绽放最鲜艳的花，我欣赏这样的人的心理，当然拒绝粗鲁地对待一切。
正想着，他居然告诉我已经尝试完了。这怎么可能？这可一共有.......多少种方案来着？
众所周知的是，我的智商很低。
我想知道种花的方案一共有几种。

输入：

仅一行，包含两个整数，分别为N和M。

输出：

仅一行，包含一个整数，表示方案数。这个数可能很大，你只需要输出这个数对1000000007取模的结果。

样例输入：

3 3

样例输出：

6

数据范围：

对于20%的数据，0<N≤5，1<M≤5
对于60%的数据，0<N≤500,000
对于100%的数据，0<N≤10^18，1<M≤10^9

【思路】

其实这种一看就知道有结论或者有公式的题，最佳的做法就是先打出暴力程序，然后把暴力的结果用表格或者图像表示出来

然后你会惊奇的发现，你要的和你不要的东东都出现在图纸上了，然后你就可以愉快的开始推公式结论了

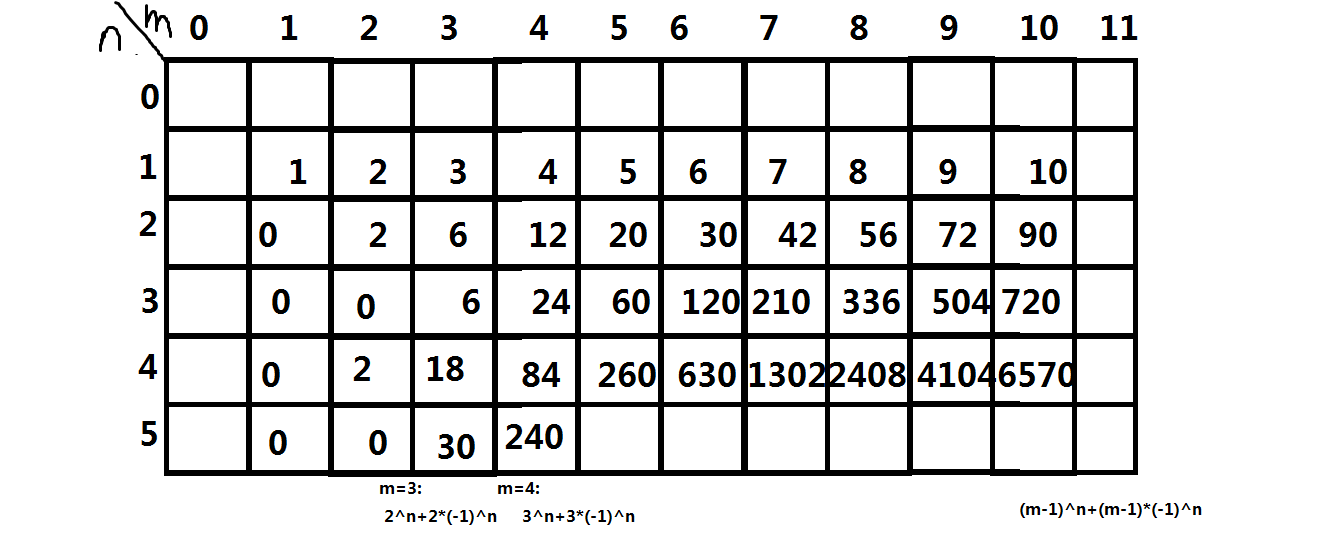
然后愉快的公式就跃然纸上。。。。

至于推这个公式，其实可以用数列推的，不过我没有那么做，我是先假设m=3，然后n在变换，推出公式，没错当m固定时，推出公式就明显是一道数学题了，接着对4进行推导，然后猜测m是未知数的情况并举例（时间不足才这样做，时间充足最好认真梳理并推导）

最后的结果就是(m-1)^n+(m-1)*(-1)^n;

到这里方法就很明显了，就是把n，m带进去，但是要注意一点，就是n是10^18次方这个范围，直接处理会爆掉，所以可以选择快速幂

快速幂的模板是

 int pow(int x,int y){
         int ans=;
     while(y){
         if(y&)ans*=x;
         x*=x;y>>=;
     }
         return ans;
 }

快速幂模板

然后这题就完了，直接输出即可，记得随时运算随时取模哦

 #include<iostream>
 #define mod 1000000007
 using namespace std;
 long long n,m,f;
 long long pow(long long x,long long y){
         long long ans=;
     while(y){
         if(y&)ans=((ans%mod)*(x%mod))%mod;
         x=((x%mod)*(x%mod))%mod;
                 y>>=;
     }
         return ans;
 }
 int main(){
     cin>>n>>m;//(m-1)^n+(m-1)*(-1)^n
     if(n==){cout<<m;return ;}
     if(n&)f=-;else f=;
     long long ans=((f%mod)*((m-)%mod))%mod;
     long long sum=pow(m-,n)%mod;
     cout<<(ans+sum+mod)%mod;
 }

正片