prim /kruskal 最小生成树

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<stack>
#include<queue>
#include<vector>
#include<time.h>
#define INF 0x3f3f3f
using namespace std;
int edge[][];
int lowcost[];
int index[];
int v,e,a,b,c;
void prim()
{
    int minm,idx;
    index[]=;
    lowcost[]=;
    for(int i=; i<v; i++)
    {
        lowcost[i]=edge[i][];
        index[i]=;
    }//初始化
    for(int i=; i<v; i++)
    {
     //   cout<<endl;
        minm=INF;
        for(int j=; j<v; j++)
        {
            // cout<<"=============="<<j<<"  "<<lowcost[j]<<endl;
            if(lowcost[j]!=&&lowcost[j]<minm)
            {
                minm=lowcost[j];
                idx=j;
               // cout<<idx<<endl;
            }

        }
      //  cout<<index[idx]<<" , "<<idx<<"   "<<lowcost[idx]<<endl;
        lowcost[idx]=;

        for(int j=; j<v; j++)
        {
            if(lowcost[j]!=&&edge[j][idx]<lowcost[j])
            {

                lowcost[j]=edge[j][idx];
                index[j]=idx;
                //cout<<"j  "<<j<<endl;
            }

        }
    }
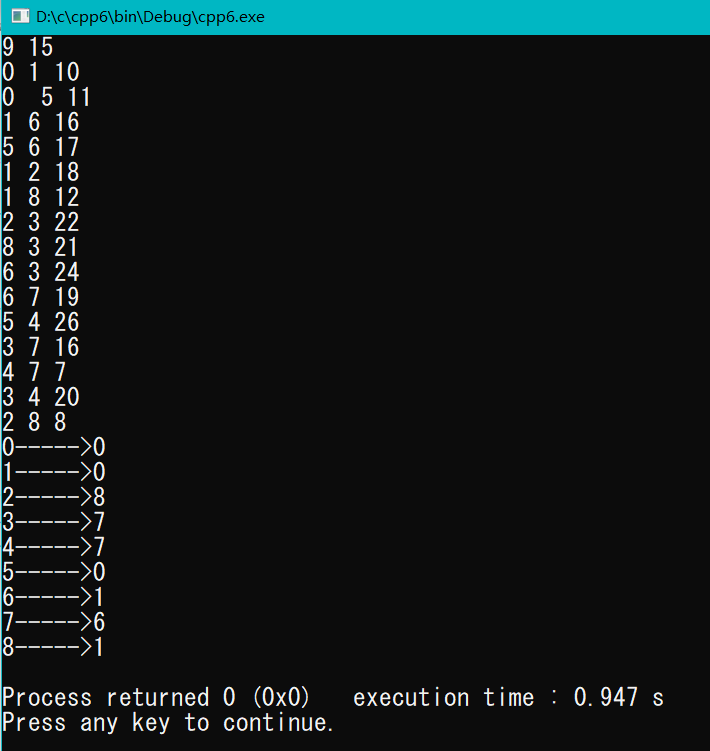
    for(int i=; i<v; i++)
    {
        cout<<i<<"----->"<<index[i]<<endl;
    }

}

int main()
{

    cin>>v>>e;
    memset(edge,INF,sizeof(edge));
    for(int i=; i<e; i++)
    {
        cin>>a>>b>>c;
        edge[a][b]=edge[b][a]=c;
    }
    prim();

}

/*

9 15
0 1 10
0 5 11
1 6 16
5 6 17
1 2 18
1 8 12
2 3 22
8 3 21
6 3 24
6 7 19
5 4 26
3 7 16
4 7 7
3 4 20
2 8 8

*/

kruskal

#include <stdio.h>
#include<iostream>
#include<algorithm>
using namespace std;
typedef struct ae
{
    int f,t,w;
} eg;
eg edge[];
int parent[];
int m,n,a,b,c;//m个点，n条边
int cmp(eg a,eg b )
{
    return a.w<b.w;
}

int find(int f)
{
    while(parent[f]>)
        f=parent[f];
    return f;
}

void kruskal()
{
    sort(edge,edge+n,cmp);
    for(int i=; i<m; i++)
        parent[i]=;
    for(int i=; i<n; i++)
    {
       int  bg=find(edge[i].f);
       int  ed=find(edge[i].t);
        if(bg!=ed)
        {
            parent[bg]=ed;
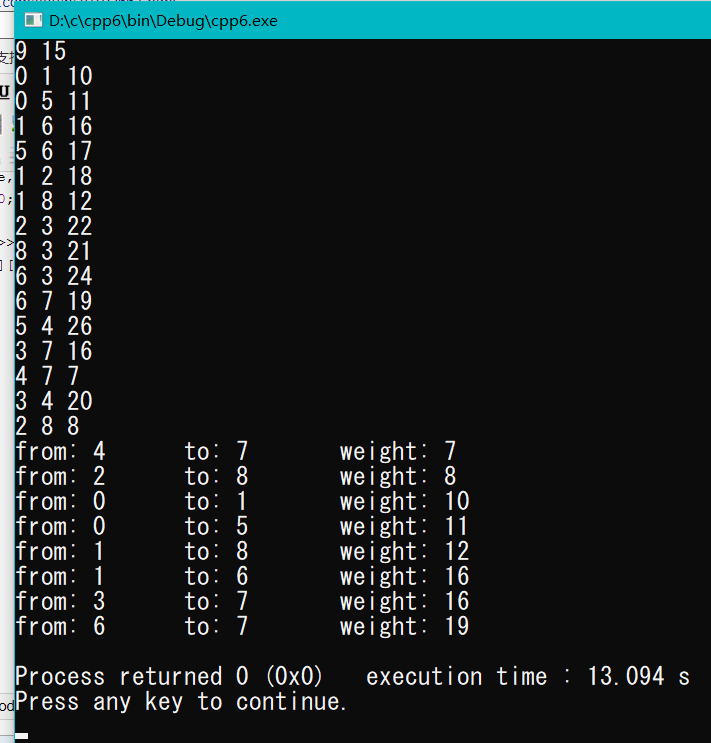
            printf("from: %d      to: %d       weight: %d\n",edge[i].f,edge[i].t,edge[i].w);
        }
    }
}

int main()
{

    cin>>m>>n;
    for(int i=; i<n; i++)
    {
        scanf("%d%d%d",&a,&b,&c);
        edge[i].f=a;edge[i].t=b;edge[i].w=c;
    }
    kruskal();
}

/*
有错
4 4
1 0 1
2 0 2
2 3 4
1 3 3
*/