Common Knowledge

2014-08-23 11:01:11

-6：四面体

（1）内切球半径：r = 3V / (S1+S2+S3+S4)

（2）体积：将四点组成三个向量AB,AC,AD,向量的混合积就是它们组成的平行六面体的体积,四面体体积是其体积的1/6。

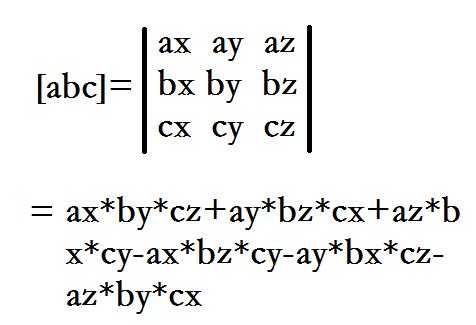
-5：枚举一个集合（设为s）的所有超集，总共N个物品。（ts为集间差）

for(int f = s; f < ( << N); f = (f + ) | s){
    int ts = s ^ f;

}

-4：枚举一个集合（设为s）的所有非空子集，总共N个物品。（ts为集间差），注意空集需要另外讨论。

for (int f = s; f > ; f = (f - ) & s) {
    int ts = s ^ f;

}

-2：头文件便利贴（C++11）

#include <bits/stdc++.h>
using namespace std;

#define getmid(l,r) ((l) + ((r) - (l)) / 2)
#define MEM(a,b) memset(a,b,sizeof(a))
#define MP(a,b) make_pair(a,b)
#define PB push_back

typedef long long ll;
typedef pair<int,int> pii;
const double eps = 1e-;
const int INF = ( << ) - ;
const int MAXN = ;

int main(){

    return ;
}

-3：头文件便利贴

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>
#include <vector>
#include <map>
#include <set>
#include <stack>
#include <queue>
#include <string>
#include <iostream>
#include <algorithm>
using namespace std;

#define getmid(l,r) ((l) + ((r) - (l)) / 2)
#define MEM(a,b) memset(a,b,sizeof(a))
#define MP(a,b) make_pair(a,b)
#define PB push_back

typedef long long ll;
typedef pair<int,int> pii;
const double eps = 1e-;
const int INF = ( << ) - ;

-1：vim配置文件

set nu ci si ai mouse=a ts= sts= sw= cursorline

0：数论

　　（1）计算比m小，且与m互质的的正整数的和：phi(m)*m/2

　　（2）计算比m小，且与m不互质的正整数的和：(phi(m)+1)*m/2

　　（3）同余符号： ≡

　　（4）1和任何数都成倍数关系，但和任何数都互质。

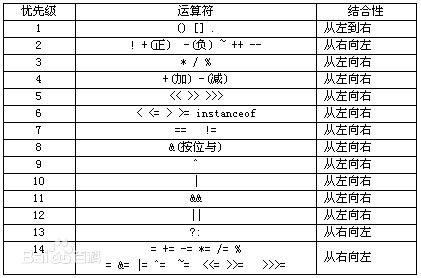
1：运算符优先级

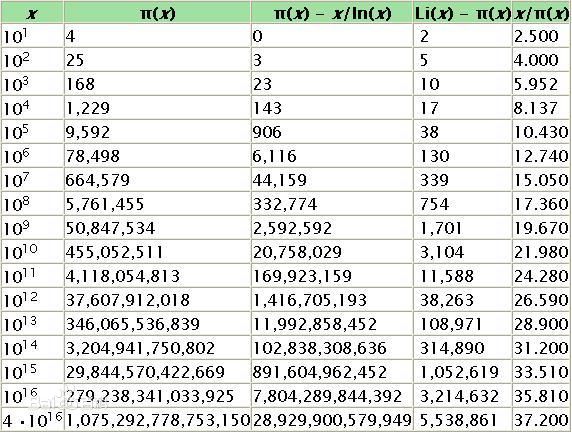
2：素数定理

3：反素数表

1,2,4,6,12,24,36,48,60,120,180,240,360,720,840,1260,1680,2520,5040,7560,10080,15120,20160,25200,27720,45360,50400,55440,83160,110880,166320,221760,277200,332640,498960,554400

4：点旋转坐标公式：

　任意点(x,y)，绕一个坐标点(rx0,ry0)逆时针旋转a角度后的新的坐标设为(x0, y0)，有公式：

x0= (x - rx0)*cos(a) - (y - ry0)*sin(a) + rx0 ;

y0= (x - rx0)*sin(a) + (y - ry0)*cos(a) + ry0 ;

5：快速读入：

inline int Read(){
      int x = ,f = ;char ch = getchar();
      while(ch < '' || ch > ''){if(ch == '-')f = -;ch = getchar();}
      while(ch >= '' && ch <= ''){x = x *  + ch - '';ch = getchar();}
      return x * f;
}

6：关闭C++读入同步

ios::sync_with_stdio(false);

7：快速输出：

void Write(int v){
      if(v>) Write(v/);
      putchar(v%+'');
}

8：正无穷

（1）int型边界：const int INF = ~0U >> 1;

9：简洁的组合数打表（from wjmzbmr）：　

for (int i = ; i < ; ++i) {
     for (int j = ; j <= i; ++j) {
          comb[i][j] =
                 (i ==  || j == ) ?
                          : (comb[i - ][j] + comb[i - ][j - ]);
     }
}

10：循环版求gcd（from tourist）

int gcd(int a, int b) {
  while (a >  && b > )
    if (a > b) a %= b;
    else b %= a;
  return a + b;
}

11：atoi 和 itoa 函数  参考：博文

　　● atoi()：将字符串转换为整型值。
　　● atol()：将字符串转换为长整型值。

　　● itoa()：将整型值转换为字符串。
　　● ltoa()：将长整型值转换为字符串。

12：卡哈希

　　参考codeforces博文

　　参考bzoj题目

13：unique函数的一些注意点：

　　数组下标从0开始：int sz = unique(a,a + n) - a;

　　数组下标从1开始：int sz = unique(a + 1,a + n + 1) - a - 1;

14：生成 long long 范围 内的随机数：（不确定是否正确）

val = ((ll)rand() << ) + ((ll)rand() << ) + ;

15：快速预处理阶乘逆元

　　先求出 （MAXN - 1）！ 的逆元，然后倒序依次求出：(MAXN - 2)！ ~ 1！ 的逆元

　　注意：如果MAXN - 1 >= mod，那么不能直接这么用。因为 fac[mod] % mod = 0

int fac[MAXN],afac[MAXN];

int Q_pow(int x,int y){
    int res = ;
    while(y){
        if(y & ) res = 1ll * res * x % mod;
        x = 1ll * x * x % mod;
        y >>= ;
    }
    return res % mod; //小心模数为1的情况
}

void Pre(){
    fac[] = afac[] = ;
    for(int i = ; i < MAXN; ++i) fac[i] = 1ll * fac[i - ] * i % mod;
    afac[MAXN - ] = Q_pow(fac[MAXN - ],mod - );
    for(int i = MAXN - ; i > ; --i) afac[i - ] = 1ll * afac[i] * i % mod;
}

16：内联汇编快速乘法

inline ll mulmod(ll x, ll y, ll mod)
{
    ll ret = ;
    __asm__("movq %1,%%rax\n imulq %2\n idivq %3\n":"=d"(ret):"m"(x),"m"(y),"m"(mod):"%rax");
    return ret;
}

17：扩栈命令

#pragma comment(linker, "/STACK:102400000,102400000")

18：fread 快速读入黑科技

const int BUFSIZE=<<; //根据题目数据而定
char Buf[BUFSIZE+],*buf=Buf;
template<class T>
inline void scan(T&a){
  for (a=;*buf<''||*buf>'';buf++);
  while (*buf>=''&&*buf<=''){a=a*+(*buf-'');buf++; }
}

fread(Buf,,BUFSIZE,stdin); //加到main函数第一行

19：根据日期算星期（基姆拉尔森公式），1~6对应星期一~星期六，0对应星期日

 int Cal(int d,int m,int y){
     if(m <= ) m += ,y--;
     return (d +  +  * m +  * (m + ) /  + y + y /  - y /  + y / ) % ;
 }

20：卡特兰数

数列：1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796

h(n)=h(n-1)*(4*n-2)/(n+1);

h(n)=C(2n,n)/(n+1) (n=0,1,2,...)

21：默慈金数

数列：1, 2, 4, 9, 21, 51, 127, 323, 835, 2188, 5798

与卡特兰数的联系：