L2-006 树的遍历 （后序中序求层序）

题目：

给定一棵二叉树的后序遍历和中序遍历，请你输出其层序遍历的序列。这里假设键值都是互不相等的正整数。

输入格式：

输入第一行给出一个正整数N（≤30），是二叉树中结点的个数。第二行给出其后序遍历序列。第三行给出其中序遍历序列。数字间以空格分隔。

输出格式：

在一行中输出该树的层序遍历的序列。数字间以1个空格分隔，行首尾不得有多余空格。

输入样例：

7
2 3 1 5 7 6 4
1 2 3 4 5 6 7

输出样例：

4 1 6 3 5 7 2

思路：

前序：根左右

后序：左右根

中序：左根右

依然是区间递归：由后序遍历的规则可知，一个树的遍历的最后一位就是该树的根结点，所以我们只需在中序遍历中找到该根结点即可在中序遍历中分出左右子树，然后左右子树再分别进行递归。如果题目要求的是先序遍历的话只需每层遍历输出根节点即可，但是题目要求输出层序遍历。我们可以建立一个数组level，初值全部设为-1，表示没有结点，将每一层的根节点存入数组的相应位置，然后按顺序输出非-1的元素就能得到层序遍历。

题目中的二叉树不一定是完全二叉树，比如样例中的二叉树如下图中黑色实线。代码中左子树在数组level中存储根节点的位置是index*2+1，右子树是index*2+2，index其实是这两个子树对应的上一层的的根节点。下图红字代表这些结点（没有结点就是-1）在level中存放的位置。比如题目中这个树在level中应该是这样存储的：4 1 6 -1 3 5 7 -1 -1 2 -1 -1 -1 -1……，level这个数组可以理解为代表完全二叉树，相当于要把存在的结点往上面填。

思路来自：https://blog.csdn.net/liuchuo/article/details/52136236

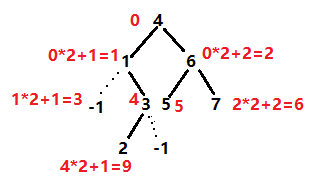
上代码：

#include <cstdio>
#include <iostream>
#include <vector>
using namespace std;
vector<int> post(),in(),level(,-);
//后序中的最后一个结点是根结点root，在中序中从start到end移动i找到这个根结点的位置，i以左是左子树，以右是右子树
void pre(int start,int end,int root,int index)//index是根节点在数组level中存放的位置
{
    if(start>end) return ;//当一个结点就是一个树时，start==end；将这个最底层的叶子结点存入level后就应该结束递归了。
    int i=start;
    while(i<end&&in[i]!=post[root]) i++;
    level[index]=post[root];
    pre(start,i-,root-(end-i)-,index*+);
    pre(i+,end,root-,index*+);
}
 
int main()
{
    int n;
    cin>>n;
    for(int i=;i<n;i++)
    {
        cin>>post[i];
    }
    for(int i=;i<n;i++)
    {
        cin>>in[i];
    }
    pre(,n-,n-,);
    int cnt=;
    for(int i=;i<;i++)
    {
        if(level[i]!=-&&cnt<n-)
        {
            cout<<level[i]<<" ";
            cnt++;
        }else if(level[i]!=-){
            cout<<level[i];
            break;
        }
    }
    return ;
}