matlab中的linkage和cluster函数

Linkage：

Agglomerative hierarchical cluster tree（凝聚成层次聚类树）

语法：

解释：

Z=linkage(x),返回Z，是一个X矩阵中行的分层聚类树（用最短距离算法生成具有层次结构的聚类树）。输入的X为pdist函数输出的距离向量矩阵（pdist函数参考上篇文章）

Z=linkage(x,method),使用指定的method创建树

Z=linkage(x,method,metric)利用度量来计算

Z=linkage(x,method,pdist_input)将参数传递给pdist函数。。。。

Z=linkage(x,method,metric,’savememory’,value)当value为true时使用一种内存保存算法，当value为false时使用标准算法。

Z=linkage(Y),用距离矩阵Y表示，Y可以是由pdist函数计算出的，也可以是一个更一般的矩阵

Z=linkage（Y,method）用指定的method创建树，method描述了 如何测量集群之间的距离。

Single:最短距离（缺省）

Complete：最大距离

Average：平均距离

Centroid：重心距离

Ward：离差平方和

输出Z:

Z是一个（m-1）-乘3矩阵，m是原始数据中行的数量。Z的第1和2列包含成对的集群索引，以形成一个二叉树。叶节点从1到m.叶节点是由所有更高的集群组成的单例集群。每一个新形成的集群，对应于第Z行（I，：），被分配索引m+I。Z（I，1:2）包含构成集群m+I的两个组件集群的索引。有m-1更高的集群，对应于集群树的内部节点。Z（I，3）包含在第Z行（I：：）中合并的两个簇之间的链接距离。

例如，假设有30个初始节点，第12步集群5和集群7合并。假设它们的距离是1。5。然后Z（12，：）是5 7 1。5。新形成的集群将有索引12+30=42。如果集群42出现在后面一行中，则意味着第12步中创建的集群将被合并到更大的集群中。

比如:

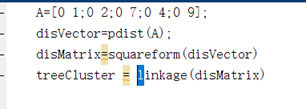
根据结果画出二叉树如下：

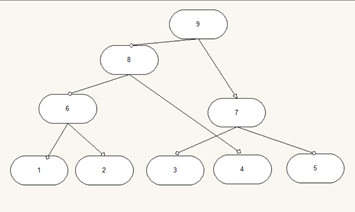
第一列，第二列为类的表示，叶子节点为原始数据的行数，1,2之间最短距离为2.2061，聚类为6（原始行数累加所得）

Cluters:

Construct agglomerative clusters from linkages(从聚类树结构中构建聚类)

语法：

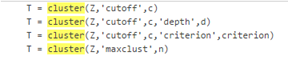
解释：

T=cluster(Z,’cutoff’,c): 从聚集的层次化集群树Z中构造集群。Z是一个大小的矩阵（m-1）-乘3(由linkage函数生成)，m是原始数据中行的数量。c是将Z切割成集群的阈值。当一个节点及其所有子节点的值都小于c时，集群就会形成，所有节点在节点或下面的所有叶子都被分组到一个集群中。t是一个大小为m的向量，包含每个观察的群集分配。如果c是一个向量，那么T是一个集群分配的矩阵，每个截止值都有一个列

T=cluster(Z,’cutoff’,c,’depth’,d): 通过观察每个节点下面的深度d来评估不一致的值。默认的深度是2。

T=cluster(Z,’cutoff’,c,’criterion’,criterion): 使用指定的标准来形成集群，其中标准是字符串“inconsistent”（默认）或“depth”。“depth”标准使用在节点上合并的两个子节点之间的距离来测量节点高度。在一个节点的高度小于c的节点的所有叶节点都被分组到一个集群中。

T=cluster(Z,’maxclust’,n): 用“depth”准则构造一个最大的n个集群。集群找到最小的高度，通过树的水平切割留下n个或更少的集群。

如果n是一个向量，那么T是一个集群分配矩阵，每个最大值是一个列。

如;

                                                 

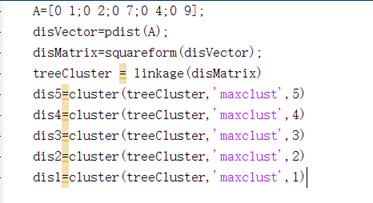
从上边的聚类树和结果的比较中可以得出，当分为5类时，每个节点单独是一类，聚成4类时，标号1和标号2聚成第4，其他单独为一类；当聚成3类时，更具聚类树，原始数据的标号3和标号5又聚成一类，一次类推。