AtCoder Regular Contest 082 E

Problem Statement

You are given N points (x_i,y_i) located on a two-dimensional plane. Consider a subset S of the N points that forms a convex polygon. Here, we say a set of points S forms a convex polygon when there exists a convex polygon with a positive area that has the same set of vertices as S. All the interior angles of the polygon must be strictly less than 180°.

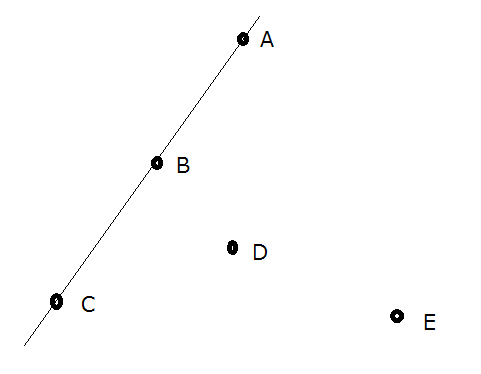
For example, in the figure above, {A,C,E} and {B,D,E} form convex polygons; {A,C,D,E}, {A,B,C,E}, {A,B,C}, {D,E} and {} do not.

For a given set S, let n be the number of the points among the N points that are inside the convex hull of S (including the boundary and vertices). Then, we will define the score of S as 2^n−|S|.

Compute the scores of all possible sets S that form convex polygons, and find the sum of all those scores.

However, since the sum can be extremely large, print the sum modulo 998244353.

Constraints

1≤N≤200
0≤x_i,y_i<10⁴(1≤i≤N)
If i≠j, x_i≠x_j or y_i≠y_j.
x_i and y_i are integers.

Input

The input is given from Standard Input in the following format:

N

x₁ y₁

x₂ y₂

:

x_N y_N

Output

Print the sum of all the scores modulo 998244353.

Sample Input 1

Copy

Sample Output 1

Copy

We have five possible sets as S, four sets that form triangles and one set that forms a square. Each of them has a score of 2⁰=1, so the answer is 5.

Sample Input 2

Copy

Sample Output 2

Copy

We have three "triangles" with a score of 1 each, two "triangles" with a score of 2 each, and one "triangle" with a score of 4. Thus, the answer is 11.

Sample Input 3

Copy

1

3141 2718

Sample Output 3

Copy

There are no possible set as S, so the answer is 0.

————————————————————————————————

题意就是求对每个凸多边形，求(2^内部点数)的和这里我们可以进行一波转换
考虑每个凸多边形，其内部的点每个都可以选择删与不删，得到的方案数就是贡献
而这个转化恰好就等价于不共线的子集数共线就是子集内所有点在同一直线上
这样之后我们只要用总的子集数减去共线的子集数就好了
枚举直线倾斜角，算包含至少两点的共线子集有几个
倾斜角用枚举两两点得到然后求gcd使得每个倾角有唯一表达形式
将向量(x,y)转为唯一表示法，然后求个hash
方便sort比较然后并查集维护这样复杂度是n^3
当然也可以把斜率离散化从sort换成散列表或者基数排序然后并查集换成连边，忽略没连到边的点就n^2了

#include<cstdio>

#include<cstring>

#include<algorithm>

const int M=,mod=;

int read(){

    int ans=,f=,c=getchar();

    while(c<''||c>''){if(c=='-') f=-; c=getchar();}

    while(c>=''&&c<=''){ans=ans*+(c-''); c=getchar();}

    return ans*f;

}

int n,f[M],sz[M];

int find(int x){while(f[x]!=x) x=f[x]=f[f[x]]; return x;}

int gcd(int x,int y){return y?gcd(y,x%y):x;}

struct pos{int x,y;}q[M];

int cnt;

struct node{

    int u,v,w;

    bool operator <(const node &x)const{return w<x.w;}

    void calc(){

        int p=find(u),q=find(v);

        if(p!=q) f[q]=p,sz[p]+=sz[q];

    }

}e[M*M];

int pw[M],ans;

void prepare(){

    pw[]=;

    for(int i=;i<=n;i++) pw[i]=(pw[i-]<<)%mod;

}

int main(){

    n=read();

    prepare(); ans=(pw[n]-n-)%mod;

    for(int i=;i<=n;i++) q[i].x=read(),q[i].y=read();

    for(int i=;i<=n;i++)

        for(int j=;j<i;j++){

            int x=q[i].x-q[j].x,y=q[i].y-q[j].y,g=gcd(x,y);

            x/=g; y/=g;

            if(!x) y=;

            if(!y) x=;

            if(x<) x=-x,y=-y;

            e[++cnt]=(node){i,j,x*+y};

        }

    std::sort(e+,e++cnt);

    for(int i=,j=;i<=cnt;i=j){

        for(int k=;k<=n;k++) sz[f[k]=k]=;

        while(j<=cnt&&e[j].w==e[i].w) e[j++].calc();

        for(int k=;k<=n;k++) if(f[k]==k&&sz[k]>=) ans=(ans-pw[sz[k]]+sz[k]+)%mod;

    }printf("%d\n",(ans+mod)%mod);

    return ;

}