[NOIp普及组2011]瑞士轮

洛谷题目链接：瑞士轮

题目背景

在双人对决的竞技性比赛，如乒乓球、羽毛球、国际象棋中，最常见的赛制是淘汰赛和循环赛。前者的特点是比赛场数少，每场都紧张刺激，但偶然性较高。后者的特点是较为公平，偶然性较低，但比赛过程往往十分冗长。

本题中介绍的瑞士轮赛制，因最早使用于1895年在瑞士举办的国际象棋比赛而得名。它可以看作是淘汰赛与循环赛的折中，既保证了比赛的稳定性，又能使赛程不至于过长。

题目描述

2*N 名编号为 1~2N 的选手共进行R 轮比赛。每轮比赛开始前，以及所有比赛结束后，都会按照总分从高到低对选手进行一次排名。选手的总分为第一轮开始前的初始分数加上已参加过的所有比赛的得分和。总分相同的，约定编号较小的选手排名靠前。

每轮比赛的对阵安排与该轮比赛开始前的排名有关：第1 名和第2 名、第 3 名和第 4名、……、第2K – 1 名和第 2K名、…… 、第2N – 1 名和第2N名，各进行一场比赛。每场比赛胜者得1 分，负者得 0 分。也就是说除了首轮以外，其它轮比赛的安排均不能事先确定，而是要取决于选手在之前比赛中的表现。

现给定每个选手的初始分数及其实力值，试计算在R 轮比赛过后，排名第 Q 的选手编号是多少。我们假设选手的实力值两两不同，且每场比赛中实力值较高的总能获胜。

输入输出格式

输入格式：

输入文件名为swiss.in 。

输入的第一行是三个正整数N、R 、Q，每两个数之间用一个空格隔开，表示有 2*N 名选手、R 轮比赛，以及我们关心的名次 Q。

第二行是2*N 个非负整数s1, s2, …, s2N，每两个数之间用一个空格隔开，其中 si 表示编号为i 的选手的初始分数。第三行是2*N 个正整数w1 , w2 , …, w2N，每两个数之间用一个空格隔开，其中 wi 表示编号为i 的选手的实力值。

输出格式：

输出文件名为swiss.out。

输出只有一行，包含一个整数，即R 轮比赛结束后，排名第 Q 的选手的编号。

输入输出样例

输入样例#1：

输出样例#1：

说明

【样例解释】

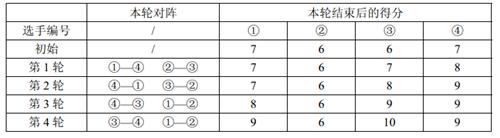
【数据范围】

对于30% 的数据，1 ≤ N ≤ 100；

对于50% 的数据，1 ≤ N ≤ 10,000 ；

对于100%的数据，1 ≤ N ≤ 100,000，1 ≤ R ≤ 50，1 ≤ Q ≤ 2N，0 ≤ s1, s2, …, s2N≤10^8，1 ≤w1, w2 , …, w2N≤ 10^8。

noip2011普及组第3题。

首先看到题目，第一眼想到的是排序模拟，然后算了一下直接快排的时间复杂度，O(nlogn+r*(nlogn+n))，感觉如果没有极限数据是可以卡过去的，然后我就意识到了这个想法是多么的愚蠢，但是事实并非如此，所以直接快排是肯定不行的．于是我们来想一下如何才能优化这个排序．

我们仔细想一下，每个比较都是从前往后依次比较过来的，那么先赢的人肯定在后赢的人前面，先输的人也一定在后输的人前面．

为什么会这样呢？我们假设数据已经是按照当前的分数排名成有序的，那么在前面的人的分数就一定比在后面的人的分数要高，那么同样是赢的人，他们的分数都会在原来基础上+1，那么先赢的人排完序之后也还是在后赢的人前面．

那么这个问题就被简化了：每次一组胜利者，一组失败者，将胜者与败者按照分数为第一关键词，编号为第二关键词来排序．既然是两组人进行合并，那么就可以用归并排序来加快时间复杂度．优化后时间复杂度O(nlogn+r*n)．

下面上代码：

 #include<bits/stdc++.h>

 using namespace std;

 const int N=+;

 int n, m, q;

 int id[N];

 int win[N];

 int lose[N];

 int mark[N];

 int v[N];

 bool cmp(int a,int b){

     if(mark[a] != mark[b]) return mark[a] > mark[b];

     return a < b;

 }

 int gi(){

     int ans =  , f = ; char i = getchar();

     while(i<''||i>''){if(i=='-')f=-;i=getchar();}

     while(i>=''&&i<=''){ans=ans*+i-'';i=getchar();}

     return ans * f;

 }

 void merge(){

     int i =  , j = ; id[] = ;

     while(i<=win[] && j<=lose[])

     if(cmp(win[i],lose[j])) id[++id[]] = win[i++];

     else id[++id[]] = lose[j++];

     while(i<=win[]) id[++id[]] = win[i++];

     while(j<=lose[]) id[++id[]] = lose[j++];

 }

 int main(){

     //freopen("data.in","r",stdin);

     n = gi(); m = gi(); q = gi(); n *= ;

     for(int i=;i<=n;i++) mark[i] = gi();

     for(int i=;i<=n;i++) v[i] = gi() , id[i] = i;

     sort(id+ , id+n+ , cmp);

     for(int i=;i<=m;i++){

     win[] = lose[] = ;

         for(int j=;j<=n;j+=){

             if(v[id[j]] > v[id[j+]]){

         mark[id[j]]++;

         win[++win[]] = id[j];

         lose[++lose[]] = id[j+];

         }

         else{

         mark[id[j+]]++;

         win[++win[]] = id[j+];

         lose[++lose[]] = id[j];

         }

     }

     merge();

     }

     cout << id[q] << endl;

     return ;

 }