【codevs1002】搭桥（prim）

　　题目描述：

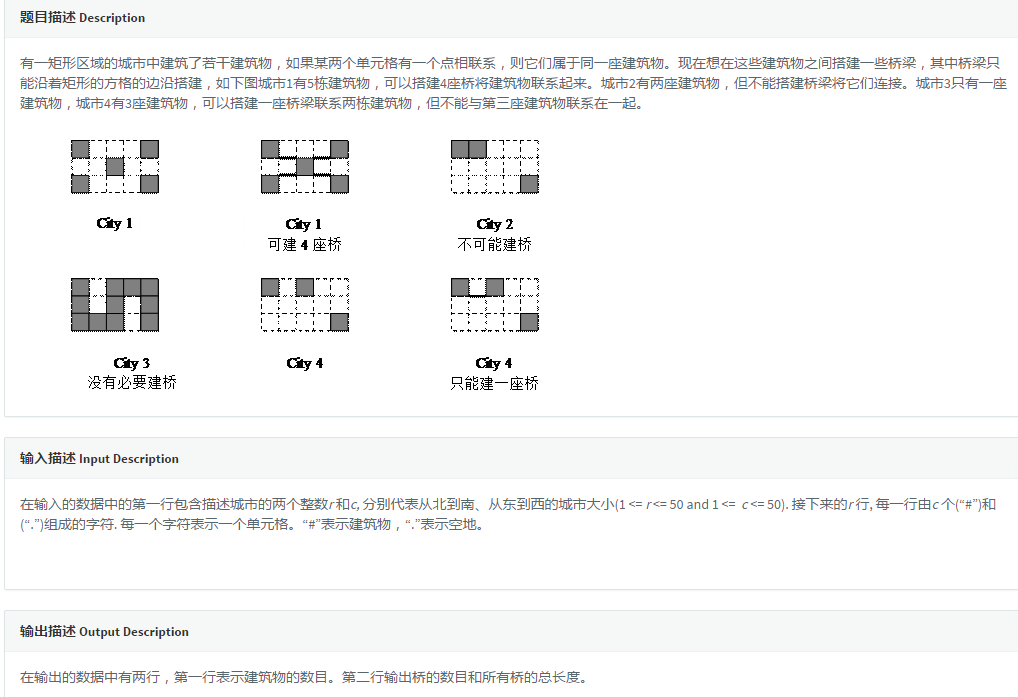
　　这是道题题意有点迷（或者是我语文不好），但其实实际上求的就是图中连通块的个数，然后在连通块与连通块之间连边建图跑最小生成树。但是……这个图可能是不连通的……求桥的数量和总长

　　于是我立刻想到了一种解法：分别在建好的图中的每一个连通块中跑最小生成树，如果当前连通块已经跑完了就跳转到下一个连通块。

　　关键代码：

for i:= to n do
    d[i]:=a[,i];
  d[]:=; sum:=; ans:=;//d[i]表示第i个点到生成树的距离，sum是桥的数量，ans是桥的总长度
  repeat
    k:=maxlongint; p:=;
    for i:= to n do
      if(d[i]<k)and(d[i]>)then begin
        k:=d[i]; p:=i;
      end;
    if p= then begin\\跳转到下一个连通块
      i:=;
      while(d[i]=)and(i<=n)do inc(i);
      if i>n then break
      else begin
        d[i]:=;
        for j:= to n do
          if(d[j]>)and(d[j]>a[i,j])then d[j]:=a[i,j];
        continue;
      end;
    end;
    ans:=ans+d[p]; inc(sum); d[p]:=;
    for i:= to n do
      if d[i]>a[p,i] then d[i]:=a[p,i];
  until false;
  writeln(sum,' ',ans);\\输出答案

　　然后我去看了看题解，发现了另外一种简单得多的方法：建假枝

　　在数据中，可能有多个建筑物，但是只要另外建一个点，将它与代表每个建筑物的点连起来（假枝），这样图就会变连通，在统计时，只要忽略假枝就能得出正确的解。

　　关键代码：

  for i:= to sum do begin\\建假枝
    a[i,sum+]:=<<;
    a[sum+,i]:=<<;
  end;
  writeln(sum); n:=sum+;
  for i:= to n do
    d[i]:=a[,i];
  d[]:=; sum:=; ans:=;
  repeat
    k:=maxlongint; p:=;
    for i:= to n do
      if(d[i]<k)and(d[i]>)then begin
        k:=d[i]; p:=i;
      end;
    if p= then break;
    if d[p]<<< then begin\\判断是否为假枝
      ans:=ans+d[p]; inc(sum);
    end;
    d[p]:=;
    for i:= to n do
      if d[i]>a[p,i] then d[i]:=a[p,i];
  until false;
  writeln(sum,' ',ans);