FJ省队集训DAY4 T1

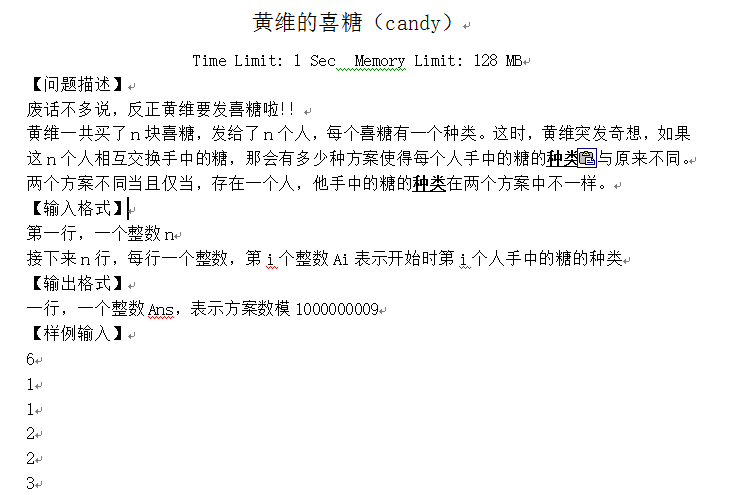
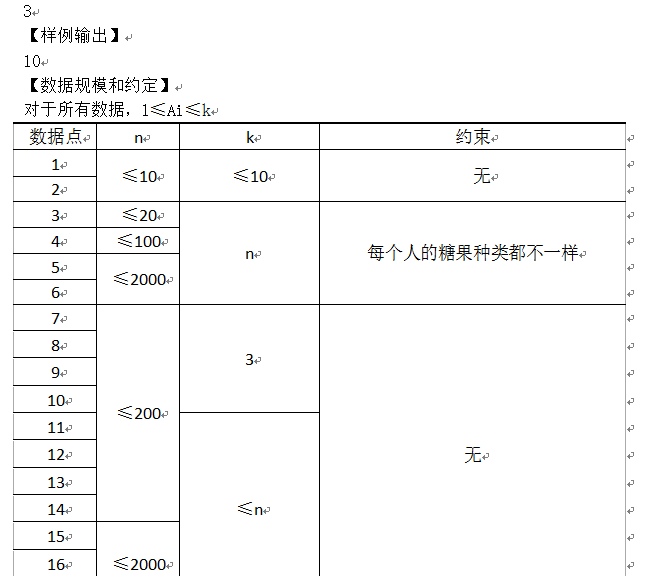
直接上题解

 #include<cstdio>
 #include<iostream>
 #include<cmath>
 #include<cstring>
 #include<algorithm>
 #define ll long long
 const int Mod=,N=;
 ll jc[N+],jcny[N+],jcnys[N+],K[N+],p[N+],f[N+];
 int read(){
     int t=,f=;char ch=getchar();
     while (ch<''||ch>''){if (ch=='-')f=-;ch=getchar();}
     while (''<=ch&&ch<=''){t=t*+ch-'';ch=getchar();}
     return t*f;
 }
 int Pow(int a,int n){
     int res=;
     while (n){
         if (n%) res=((ll)res*a)%Mod;
         a=((ll)a*a)%Mod;
         n/=;
     }
     return res;
 }
 int main(){
     jc[]=;
     for (int i=;i<=;i++) jc[i]=(ll)(jc[i-]*i)%Mod;
     jcny[]=Pow(jc[],Mod-)%Mod;
     for (int i=;i>=;i--) jcny[i]=(ll)jcny[i+]*(i+)%Mod;
     for (int i=;i<=;i++) jcnys[i]=(ll)jcny[i]*jcny[i]%Mod;
     for (int i=;i<=;i++)
      if ((i&)&&jcny[i]) K[i]=Mod-jcny[i];else K[i]=jcny[i];
     int n=read();
     for (int i=;i<=n;i++) {
         int x=read();p[x]++;
     }
     f[]=;
     for (int k=,tot=;k<=n;k++){
         if (p[k]==) continue;
         tot+=p[k];
         for (int i=tot;i>=;i--){
             f[i]=(ll)f[i]*jcnys[p[k]]%Mod;
             for (int j=;j<=p[k]&&j<=i;j++)
              f[i]=((ll)f[i-j]*K[j]%Mod*jcnys[p[k]-j]+f[i])%Mod;
         }
     }
     ll ans=;
     for (int i=;i<=n;i++)
      ans=((ll)jc[n-i]*f[i]+ans)%Mod;
     for (int i=;i<=n;i++)
      ans=(ll)ans*jc[p[i]]%Mod;
     printf("%I64d\n",ans);
 }