Luogu P1712 [NOI2016]区间(线段树)

P1712 [NOI2016]区间

题意

题目描述

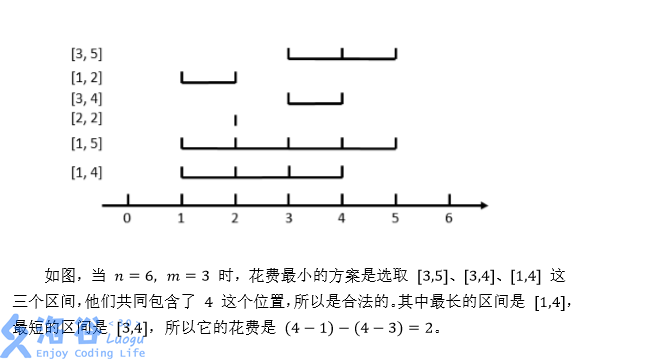
在数轴上有 \(N\) 个闭区间 \([l_1,r_1],[l_2,r_2],...,[l_n,r_n]\) 。现在要从中选出 \(M\) 个区间，使得这 \(M\) 个区间共同包含至少一个位置。换句话说，就是使得存在一个 \(x\) ，使得对于每一个被选中的区间 \([l_i,r_i]\) ，都有 \(l_i \leq x \leq r_i\) 。

对于一个合法的选取方案，它的花费为被选中的最长区间长度减去被选中的最短区间长度。区间 \([l_i,r_i]\) 的长度定义为 \(r_i-l_i\) ，即等于它的右端点的值减去左端点的值。

求所有合法方案中最小的花费。如果不存在合法的方案，输出 \(-1\) 。

输入输出格式

输入格式：

第一行包含两个正整数 \(N,M\) 用空格隔开，意义如上文所述。保证 \(1 \leq M \leq N\)

接下来 \(N\) 行，每行表示一个区间，包含用空格隔开的两个整数 \(l_i\) 和 \(r_i\) 为该区间的左右端点。

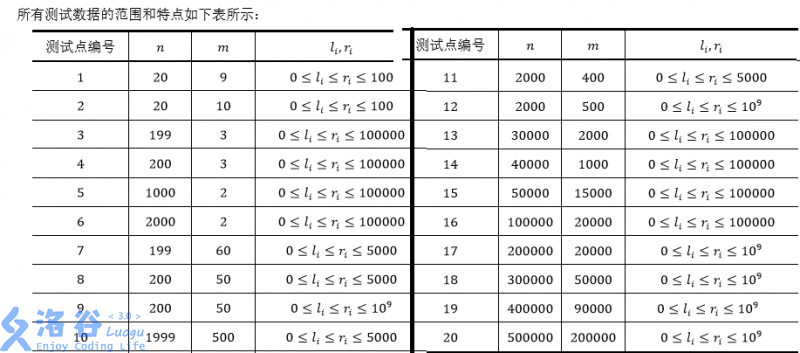
\(N \leq 500000,M \leq 200000,0 \leq l_i \leq r_i \leq 10^9\)

输出格式：

只有一行，包含一个正整数，即最小花费。

输入输出样例

输入样例：

6 3
3 5
1 2
3 4
2 2
1 5
1 4

输出样例：

2

说明

思路

2018-10-6 非完美算法测试唯一的可做题，然后用 \(STL\) 瞎搞了一波，只有 \(60\) 分 \(qwq\) 。赛后学习了 logeadd 的代码，就 \(A\) 掉了。

首先按照区间长度排序，然后我们枚举排序后的 \([1,M]\) 的一段区间 \([L,R]\) ，使得这一段区间能够刚好覆盖住同一个点 \(m\) 次，那么就可以用 \(len[R]-len[L]\) 来更新答案。

枚举区间可以使用尺取法，而判断这一区间是否合法可以用线段树。对于每一个区间 \([l_i,r_i]\) ，我们在线段树上进行这个区间的区间加，然后统计区间最大值，就可以了。当然，这个数据范围是需要离散化的。

AC代码

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL MAXN=5e5+5;
LL n,m,cnt,head,tail,ans=LLONG_MAX,s[MAXN],t[MAXN],num[MAXN<<1];
struct Segment
{
    LL l,r,len;
    bool operator < (const Segment &sjf) const {return len<sjf.len;}
}seg[MAXN];
struct SegmentTree
{
    LL l,r,data,tag;
    #define l(a) tree[a].l
    #define r(a) tree[a].r
    #define d(a) tree[a].data
    #define t(a) tree[a].tag
}tree[MAXN<<3];
LL read()
{
    LL re=0;
    char ch=getchar();
    while(!isdigit(ch)) ch=getchar();
    while(isdigit(ch)) re=(re<<3)+(re<<1)+ch-'0',ch=getchar();
    return re;
}
void build(LL p,LL ll,LL rr)
{
    l(p)=ll,r(p)=rr;
    if(ll==rr) return ;
    LL mid=(ll+rr)>>1;
    build(p<<1,ll,mid);
    build(p<<1|1,mid+1,rr);
}
void pushdown(LL p)
{
    if(t(p))
    {
        d(p<<1)+=t(p),d(p<<1|1)+=t(p);
        t(p<<1)+=t(p),t(p<<1|1)+=t(p);
        t(p)=0;
    }
}
void change(LL p,LL ll,LL rr,LL k)
{
    if(ll<=l(p)&&r(p)<=rr)
    {
        t(p)+=k,d(p)+=k;
        return ;
    }
    pushdown(p);
    LL mid=(l(p)+r(p))>>1;
    if(mid>=ll) change(p<<1,ll,rr,k);
    if(mid<rr) change(p<<1|1,ll,rr,k);
    d(p)=max(d(p<<1),d(p<<1|1));
}
int main()
{
    n=read(),m=read();
    for(LL i=1;i<=n;i++) num[cnt++]=seg[i].l=read(),num[cnt++]=seg[i].r=read(),seg[i].len=seg[i].r-seg[i].l;
    sort(seg+1,seg+n+1);
    sort(num,num+cnt);
    cnt=unique(num,num+cnt)-num;
    for(LL i=1;i<=n;i++) seg[i].l=lower_bound(num,num+cnt,seg[i].l)-num,seg[i].r=lower_bound(num,num+cnt,seg[i].r)-num;
    build(1,0,cnt-1);
    while(1)
    {
        while(d(1)<m&&tail<n)
        {
            tail++;
            change(1,seg[tail].l,seg[tail].r,1);
        }
        if(d(1)<m) break;
        while(d(1)>=m&&head<n)
        {
            head++;
            change(1,seg[head].l,seg[head].r,-1);
        }
        ans=min(ans,seg[tail].len-seg[head].len);
    }
    printf("%lld",ans==LLONG_MAX?-1:ans);
    return 0;
}