OpenCASCADE点向直线投影
OpenCASCADE点向直线投影
在GeomLib_Tool类中提供了计算指定点在曲线、曲面上的参数,这个算法具有通用性,即对任意曲线、曲面来反求点的参数。
本文主要结合源码分析点向直线投影的算法。在类Extrema_ExtPElC中提供了点向基本的曲线距离极值计算的功能,基本曲线就是常见的直线、圆、椭圆、抛物线、双曲线等。其中点到直线的距离源码如下:
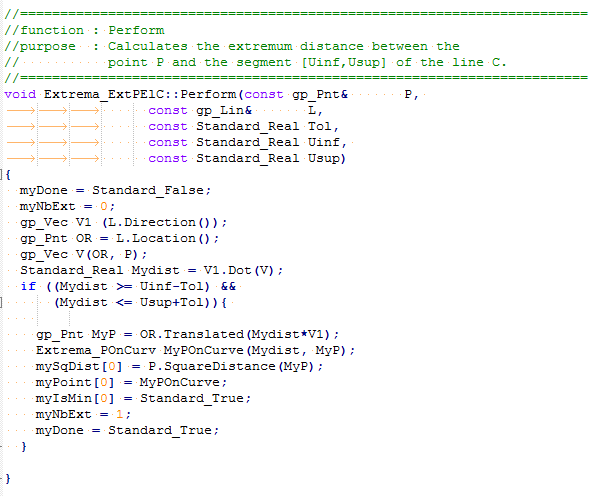
根据源码的意思画出一个图来说明会更直观,其中向量V1是直线的方向向量,V是直线的起点到点P的向量。
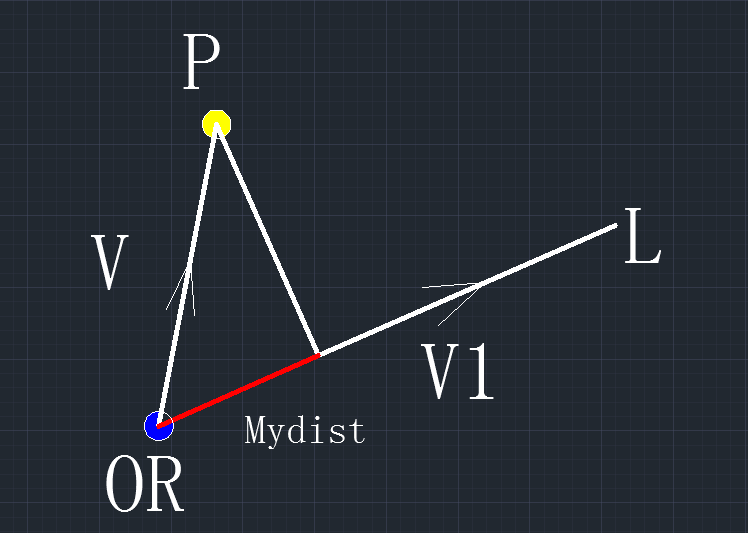
算法主要使用向量点乘得到点投影到直线上的距离Mydist,再将点OR沿着直线的方向V1移动Mydist距离就得到了点投影到直线上的点。结合源码及其注释还可以看出只有点在直线的投影点到直线原点OR的距离Mydist在指定的范围内才会保存计算结果。当有范围限制时,即是计算的点到线段的投影,无限制时就是点到直线的投影。
向量的计算有时可以简化程序而且算法性能高,充分理解向量的运算并熟练地运用是图形学编程中的基础。
OpenCASCADE点向直线投影的更多相关文章
- OpenCASCADE点向平面投影
OpenCASCADE点向平面投影 OpenCASCADE的ProjLib类提供了解析曲线(直线.圆.椭圆.抛物线.双曲线)向解析曲面(平面.圆柱面.圆锥面.球面.圆环面)投影的功能,主要用来计算三维 ...
- OpenCASCADE圆与平面求交
OpenCASCADE圆与平面求交 eryar@163.com 在 解析几何求交之圆与二次曲面中分析了OpenCASCADE提供的类IntAna_IntConicQuad可以用来计算圆与二次曲面之间的 ...
- Two analytical 2d line intersection in OpenCASCADE
Two analytical 2d line intersection in OpenCASCADE eryar@163.com Abstract. OpenCASCADE geometric too ...
- PCA算法详解——本质上就是投影后使得数据尽可能分散(方差最大),PCA可以被定义为数据在低维线性空间上的正交投影,这个线性空间被称为主⼦空间(principal subspace),使得投影数据的⽅差被最⼤化(Hotelling, 1933),即最大方差理论。
PCA PCA(Principal Component Analysis,主成分分析)是一种常用的数据分析方法.PCA通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量 ...
- Intersection between a 2d line and a conic in OpenCASCADE
Intersection between a 2d line and a conic in OpenCASCADE eryar@163.com Abstract. OpenCASCADE provid ...
- 数据降维技术(1)—PCA的数据原理
PCA(Principal Component Analysis)是一种常用的数据分析方法.PCA通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量,常用于高维数据的降 ...
- 线性代数和numpy——黑板客老师课程学习
一.代数是什么 代数->数的抽象表示->向量空间(线性空间) 线代->线性代数 关系: 向量空间之间和内部转换是通过线性变换. 实数——一维空间的点 复数——二维空间的点 如果两个向 ...
- PCA原理与实践
在对数据进行预处理时,我们经常会遇到数据的维数非常之大,如果不进行相应的特征处理,那么算法的资源开销会很大,这在很多场景下是我们不能接受的.而对于数据的若干维度之间往往会存在较大的相关性,如果能将数据 ...
- PCA的数学原理
PCA(Principal Component Analysis)是一种常用的数据分析方法.PCA通过线性变换将原始数据变换为一组各维度线性无关的表示,可用于提取数据的主要特征分量,常用于高维 数据的 ...
随机推荐
- logback日志文件的使用
1.引入Jar包,Maven pom.xml <!-- Logging with SLF4J & LogBack --> <dependency> <groupI ...
- C++: class sizeof
https://blog.csdn.net/fengxinlinux/article/details/72836199 C++中类所占的大小计算,因为涉及到虚函数成员,静态成员,虚继承,多继承以及空类 ...
- jvm虚拟内存分布 与 GC算法
jvm虚拟内存分布 程序计数器(PC寄存器)(线程私有): 每个线程启动的时候,都会创建一个PC(Program Counter,程序计数器)寄存器. PC寄存器的内容总是指向下一条将被执行指令的地址 ...
- 0920CSP-S模拟测试赛后总结
依旧挂了. 这次出题人十分良心.白送了180分……于是我没有拿到.130分rank43滚粗了. T1是道sbdp.然而我死想哈希.然后就死在哈希上了. 我简直是个傻子.之前考了几次字符串的题可以用哈希 ...
- c&c++MFC 调用 js 函数代码
调用函数代码和示例 Code highlighting produced by Actipro CodeHighlighter (freeware)http://www.CodeHighlight ...
- SpringCloud及其五大常用组件之Eureka和Zuul
1.springcloud简介 SpringCloud是Spring旗下的项目之一,它是微服务架构的一种实现方式. 官网地址:http://projects.spring.io/spring-clou ...
- vue双向绑定的原理
什么是双向数据绑定?Vue是一个MVVM框架,数据绑定简单来说,就是当数据发生变化时,相应的视图会进行更新,当视图更新时,数据也会跟着变化. 实现数据绑定的方式大致有以下几种: - 1.发布者-订阅者 ...
- mavlink 笔记1
Packet Anatomy This is the anatomy of one packet. It is inspired by the CAN and SAE AS-4 standards. ...
- multiprocessing多进程(31-04)创建进程的两种方式
一个进程可以寄生多个线程. CPU核数与进程个数是统一的, 若进程多于核数,那么只有等待上一进程执行完才能被执行. ------------------第一种进程创建方式--------------- ...
- c# Data = select new{} 返回值的显示
