洛谷P1073最优贸易（跑两遍dij）

题目描述

CC C国有n n n个大城市和m mm 条道路，每条道路连接这 nnn个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这 mmm 条道路中有一部分为单向通行的道路，一部分为双向通行的道路，双向通行的道路在统计条数时也计为 11 1条。

CC C国幅员辽阔，各地的资源分布情况各不相同，这就导致了同一种商品在不同城市的价格不一定相同。但是，同一种商品在同一个城市的买入价和卖出价始终是相同的。

商人阿龙来到 CCC 国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息之后，便决定在旅游的同时，利用商品在不同城市中的差价赚回一点旅费。设 CCC 国 n 个城市的标号从 1 n1~ n1 n，阿龙决定从 11 1号城市出发，并最终在 nnn 号城市结束自己的旅行。在旅游的过程中，任何城市可以重复经过多次，但不要求经过所有 nnn 个城市。阿龙通过这样的贸易方式赚取旅费：他会选择一个经过的城市买入他最喜欢的商品――水晶球，并在之后经过的另一个城市卖出这个水晶球，用赚取的差价当做旅费。由于阿龙主要是来 CCC 国旅游，他决定这个贸易只进行最多一次，当然，在赚不到差价的情况下他就无需进行贸易。

假设 CC C国有 555个大城市，城市的编号和道路连接情况如下图，单向箭头表示这条道路为单向通行，双向箭头表示这条道路为双向通行。

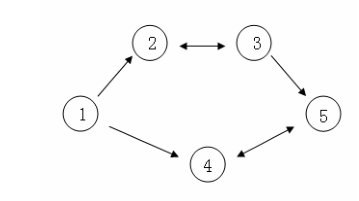
假设 1 n1~n1 n 号城市的水晶球价格分别为 4,3,5,6,14,3,5,6,14,3,5,6,1。

阿龙可以选择如下一条线路：111->222->333->555，并在 22 2号城市以3 33 的价格买入水晶球，在 333号城市以5 5 5的价格卖出水晶球，赚取的旅费数为 2。

阿龙也可以选择如下一条线路1 11->444->555->444->555，并在第11 1次到达5 55 号城市时以 11 1的价格买入水晶球，在第 222 次到达4 44 号城市时以6 66 的价格卖出水晶球，赚取的旅费数为5 55。

现在给出 nn n个城市的水晶球价格，mmm 条道路的信息（每条道路所连接的两个城市的编号以及该条道路的通行情况）。请你告诉阿龙，他最多能赚取多少旅费。

输入格式

第一行包含 222 个正整数n n n和 mmm，中间用一个空格隔开，分别表示城市的数目和道路的数目。

第二行 n 个正整数，每两个整数之间用一个空格隔开，按标号顺序分别表示这 n 个城市的商品价格。

接下来 mmm 行，每行有3 3 3个正整数x,y,zx,y,zx,y,z，每两个整数之间用一个空格隔开。如果 z=1z=1z=1，表示这条道路是城市x x x到城市y y y之间的单向道路；如果z=2 z=2z=2，表示这条道路为城市 xx x和城市yy y之间的双向道路。

输出格式

一个整数，表示最多能赚取的旅费。如果没有进行贸易，则输出 000。

输入输出样例

输入 #1

输出 #1

说明/提示

【数据范围】

输入数据保证 111 号城市可以到达n n n号城市。

对于 10%的数据，1≤n≤61≤n≤61≤n≤6。

对于 30%的数据，1≤n≤1001≤n≤1001≤n≤100。

对于 50%的数据，不存在一条旅游路线，可以从一个城市出发，再回到这个城市。

对于 100%的数据，1≤n≤1000001≤n≤1000001≤n≤100000，1≤m≤5000001≤m≤5000001≤m≤500000，1≤x1≤x1≤x，y≤ny≤ny≤n，1≤z≤21≤z≤21≤z≤2，1≤1≤1≤各城市

水晶球价格≤100≤100≤100。

NOIP 2009 提高组第三题

将双向边存储为两条单向边，建一张原图一张反图，跑两边dijkstra（或者spfa）。第一遍求数组d，d[x]表示从1到x的所有路径中经过的权值最小的节点的权值。第二遍求数组d1，d1[x]表示从n到x的所有路径中经过的权值最大的节点的权值（由单源最短路的求法可知，只能由确定的点n开始，所以必须建反图求）。然后遍历节点，ans=max(ans,d1[i]-d[i])更新答案。

#include <iostream>

#include <cstdio>

#include <queue>

#include <cstring>

#include <bits/stdc++.h>

using namespace std;

const int N=;

const int M=;

int head[N],ver[M],Next[M],d[N];bool v[N];

int head1[N],ver1[M],Next1[M],d1[N];bool v1[N];

int price[N];

int n,m,tot=,tot1=;

void add(int x,int y)

{

    ver[++tot]=y;

    Next[tot]=head[x];

    head[x]=tot;

}

void add1(int x,int y)

{

    ver1[++tot1]=y;

    Next1[tot1]=head1[x];

    head1[x]=tot1;

}

priority_queue< pair<int,int> >q;

priority_queue< pair<int,int> >q1;

void dij()

{

    memset(d,0x3f,sizeof(d));

    memset(v,,sizeof(v));

    d[]=price[];//一定要注意初始化！！！！！！！！！ 千万不能加v[1]=1;!!!!!!

    q.push(make_pair(price[],));

    while(q.size())

    {

        int x=q.top().second;q.pop();

        if(v[x])continue;

        v[x]=;

        int i;

        for(i=head[x];i;i=Next[i])

        {

            int y=ver[i];

            d[y]=min(d[x],price[y]);

            q.push(make_pair(d[y],y));

        }

    }

 }

 void dij1()

{

    memset(d1,-0x3f,sizeof(d1));//初始化为负无穷

    memset(v1,,sizeof(v1));

    d1[n]=price[n];//v1[n]=1;//千万不能加这一条

    q1.push(make_pair(price[n],n));

    while(q1.size())

    {

        int x=q1.top().second;q1.pop();

        if(v1[x])continue;

        v1[x]=;

        int i;

        for(i=head1[x];i;i=Next1[i])

        {

            int y=ver1[i];

            d1[y]=max(d1[x],price[y]);

            q1.push(make_pair(d1[y],y));

        }

    }

 }

 int main()

 {

     cin>>n>>m;

     int i;

     for(i=;i<=n;i++)

     {

         scanf("%d",&price[i]);

     }

     for(i=;i<=m;i++)

     {

         int x,y,z;

         scanf("%d%d%d",&x,&y,&z);

         if(z==)

         {

             add(x,y);

             add1(y,x);

         }

         else

         {

             add(x,y);add(y,x);

             add1(x,y);add1(y,x);

         }

     }

     dij();

     dij1();

     int ans=;

     for(i=;i<=n;i++)

     {

         ans=max(ans,d1[i]-d[i]);

     }

     cout<<ans;

     return ;

  }