计蒜客NOIP模拟赛4 D1T3 小X的佛光

小 X 是远近闻名的学佛，平日里最喜欢做的事就是蒸发学水。

小 X 所在的城市 X 城是一个含有 N 个节点的无向图，同时，由于 X 国是一个发展中国家，为了节约城市建设的经费，X 国首相在建造 X 城时只建造 N – 1 条边，使得城市的各个地点能够相互到达。

小 X 计划蒸发 Q 天的学水，每一天会有一名学水从 A 地走到 B 地，并在沿途各个地点留下一个水塘。此后，小 X 会从 C 地走到 B 地，并用佛光蒸发沿途的水塘。由于 X 城是一个学佛横行的城市，学水留下的水塘即使没有被小 X 蒸发，也会在第二天之前被其他学佛蒸发殆尽。

现在，小 X 想要知道，他每一天能够蒸发多少水塘呢?

输入格式

第一行三个整数 N,Q,num，分别表示 X 城地点的个数，小 X 蒸发学水的天数，以及测试点编号。注意，测试点编号是为了让选手们更方便的获得部分分，你可能不需要用到这则信息，在下发的样例中，测试点编号的含义是该样例满足某一测试点限制。

接下来 N – 1 行，每行两个整数 X,Y，表示 X 地与 Y 地之间有一条边。

接下来 Q 行，每行三个整数 A,B,C，表示一天中，有一名学水从 A 地走到 B 地，而小 X 会从 C 地走到 B 地。

输出格式

输出 Q 行，每行一个整数，表示小 X 能够蒸发的水塘数。

数据规模与约定

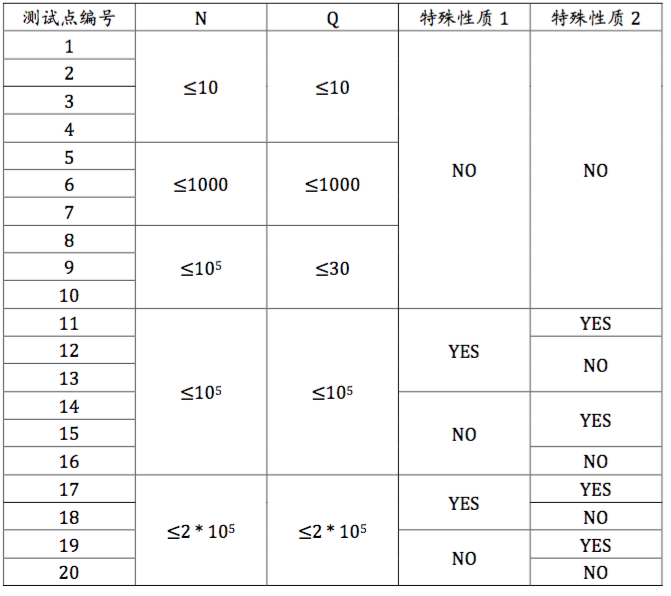
特殊性质 1：第 i 条边连接第 i 和第 i+1 个地点。

特殊性质 2：A=C。

样例输入

样例输出

1
1
3
A->B与B->C的共同路径长为
(LAB+LBC-LAC)/2
不过因为是点权，所以要+1
直接倍增LCA就行了
不过建树不能用dfs，会溢出，要用bfs()

 #include<iostream>
 #include<algorithm>
 #include<cstdio>
 #include<cstring>
 #include<queue>
 using namespace std;
 struct Node
 {
     int next,to;
 }edge[];
 int num,head[];
 int n,q,dep[],fa[][];
 bool vis[];
 void add(int u,int v)
 {
     num++;
     edge[num].next=head[u];
     head[u]=num;
     edge[num].to=v;
 }
 void bfs()
 {int i;
  queue<int>Q;
  memset(vis,,sizeof(vis));
   dep[]=;
  Q.push();
  vis[]=;
   while (Q.empty()==)
   {
       int u=Q.front();
       Q.pop();
       for (i=head[u];i;i=edge[i].next)
       {
           int v=edge[i].to;
           if (vis[v]==)
           {
               vis[v]=;
               dep[v]=dep[u]+;
               fa[v][]=u;
               Q.push(v);
           }
       }
   }
 }
 int LCA(int x,int y)
 {int i;
     if (dep[x]<dep[y]) swap(x,y);
     for (i=;i>=;i--)
         if ((<<i)<=dep[x]-dep[y]) x=fa[x][i];
  if (x==y) return x;
  while (x!=y)
  {
     for (i=;i>=;i--)
         if (fa[x][i]!=fa[y][i])
         {
             x=fa[x][i];
             y=fa[y][i];
         }
 
     if (x==y) return x;
     x=fa[x][];
     y=fa[y][];
  }
     return x;
 }
 int main()
 {int x,y,i,a,b,c,j;
     cin>>n>>q>>x;
     for (i=;i<=n-;i++)
     {
         scanf("%d%d",&x,&y);
         add(x,y);add(y,x);
     }
      bfs();
  for (i=;i<=n;i++)
     {
      for (j=;j<=;j++)
          fa[i][j]=fa[fa[i][j-]][j-];
     }
     for (i=;i<=q;i++)
     {
         scanf("%d%d%d",&a,&b,&c);
         int l1=LCA(a,b),l2=LCA(b,c),l3=LCA(a,c);
         int s1=dep[a]-dep[l1]+dep[b]-dep[l1];
         int s2=dep[b]-dep[l2]+dep[c]-dep[l2];
         int s3=dep[a]-dep[l3]+dep[c]-dep[l3];
         printf("%d\n",(s1+s2-s3)/+);
     }
 }