理解滑动平均(exponential moving average)

1. 用滑动平均估计局部均值

　　滑动平均(exponential moving average)，或者叫做指数加权平均(exponentially weighted moving average)，可以用来估计变量的局部均值，使得变量的更新与一段时间内的历史取值有关。

　　变量$v$在$t$时刻记为$v_t$，$\theta_t$为变量$v$在$t$时刻的取值，即在不使用滑动平均模型时$v_t = \theta_t$，在使用滑动平均模型后，$v_t$的更新公式如下：

\begin{equation} v_t = \beta*v_{t-1} + (1 - \beta) * \theta_t \end{equation}

　　上式中，$\beta \in [0,1)$。$\beta = 0$ 相当于没有使用滑动平均。

　　假设起始$v_0= 0$，$\beta = 0.9$，之后每个时刻，依次对变量$v$进行赋值，不使用滑动平均和使用滑动平均结果如下：

表 1

t	不使用滑动平均模型，即给$v$直接赋值$\theta$	使用滑动平均模型，按照公式(1)更新$v$	使用滑动平均模型，按照公式(2)更新$v$
0	0	/	/
1	10	1	10
2	20	2.9	13.6842
3	10	3.61	13.3210
4	0	3.249	9.4475
5	10	3.9241	9.5824
6	20	5.53169	11.8057
7	30	7.978521	15.2932
8	5	7.6806689	13.4859
9	0	6.91260201	11.2844

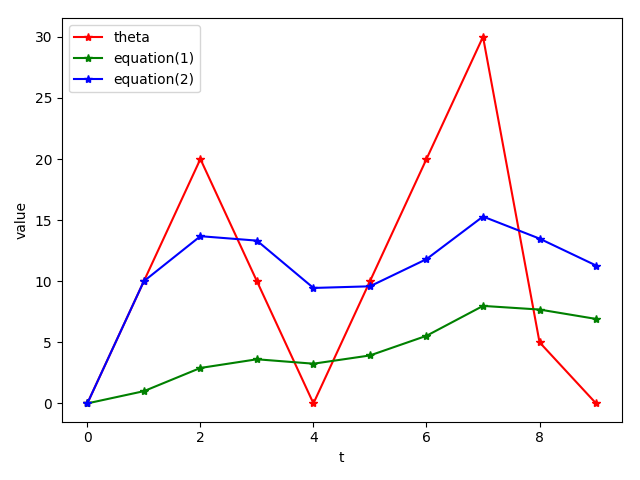
图 1：三种变量更新方式

　　Andrew Ng在Course 2 Improving Deep Neural Networks中讲到，$t$时刻变量$v$的滑动平均值大致等于过去$1/(1 - \beta)$个时刻$\theta$值的平均。这个结论在滑动平均起始时相差比较大，所以有了Bias correction，将$v_t$除以$(1 - \beta^t)$修正对均值的估计。

　　加入了Bias correction后，$v_t$更新公式如下：

\begin{equation} v_t = \frac{\beta*v_{t-1} + (1 - \beta) * \theta_t}{1 - \beta^t} \end{equation}

$t$越大，$1-\beta^t$越接近1，则公式(1)和(2)得到的结果将越来越近。

　　当$\beta$越大时，滑动平均得到的值越和$\theta$的历史值相关。如果$\beta = 0.9$，则大致等于过去10个$\theta$值的平均；如果$\beta = 0.99$，则大致等于过去100个$\theta$值的平均。

　　滑动平均的好处：

占内存少，不需要保存过去10个或者100个历史$\theta$值，就能够估计其均值。（当然，滑动平均不如将历史值全保存下来计算均值准确，但后者占用更多内存和计算成本更高）

2. TensorFlow中使用滑动平均来更新变量（参数）

　　滑动平均可以看作是变量的过去一段时间取值的均值，相比对变量直接赋值而言，滑动平均得到的值在图像上更加平缓光滑，抖动性更小，不会因为某次的异常取值而使得滑动平均值波动很大，如图 1所示。

　　TensorFlow 提供了 tf.train.ExponentialMovingAverage 来实现滑动平均。在初始化 ExponentialMovingAverage 时，需要提供一个衰减率（decay），即公式(1)(2)中的$\beta$。这个衰减率将用于控制模型的更新速度。ExponentialMovingAverage 对每一个变量（variable）会维护一个影子变量（shadow_variable），这个影子变量的初始值就是相应变量的初始值，而每次运行变量更新时，影子变量的值会更新为：

\begin{equation} \mbox{shadow_variable} = \mbox{decay} * \mbox{shadow_variable} + (1 - \mbox{decay}) * \mbox{variable} \end{equation}

公式(3)中的 shadow_variable 就是公式(1)中的$v_t$，公式(3)中的 variable 就是公式(1)中的$\theta_t$，公式(3)中的 decay 就是公式(1)中的$\beta$。

　　公式(3)中，decay 决定了影子变量的更新速度，decay 越大影子变量越趋于稳定。在实际运用中，decay一般会设成非常接近1的数（比如0.999或0.9999）。为了使得影子变量在训练前期可以更新更快，ExponentialMovingAverage 还提供了 num_updates 参数动态设置 decay 的大小。如果在初始化 ExponentialMovingAverage 时提供了 num_updates 参数，那么每次使用的衰减率将是：

\begin{equation} min\{\mbox{decay}, \frac{1 + \mbox{num_updates}}{10 + \mbox{num_updates}}\} \end{equation}

这一点其实和Bias correction很像。

　　TensorFlow 中使用 ExponentialMovingAverage 的例子：code

3. 滑动平均为什么在测试过程中被使用？

　　滑动平均可以使模型在测试数据上更健壮（robust）。“采用随机梯度下降算法训练神经网络时，使用滑动平均在很多应用中都可以在一定程度上提高最终模型在测试数据上的表现。”

　　对神经网络边的权重 weights 使用滑动平均，得到对应的影子变量 shadow_weights。在训练过程仍然使用原来不带滑动平均的权重 weights，不然无法得到 weights 下一步更新的值，又怎么求下一步 weights 的影子变量 shadow_weights。之后在测试过程中使用 shadow_weights 来代替 weights 作为神经网络边的权重，这样在测试数据上效果更好。因为 shadow_weights 的更新更加平滑，对于随机梯度下降而言，更平滑的更新说明不会偏离最优点很远；对于梯度下降 batch gradient decent，我感觉影子变量作用不大，因为梯度下降的方向已经是最优的了，loss 一定减小；对于 mini-batch gradient decent，可以尝试滑动平均，毕竟 mini-batch gradient decent 对参数的更新也存在抖动。

　　设$\mbox{decay} = 0.999$，一个更直观的理解，在最后的1000次训练过程中，模型早已经训练完成，正处于抖动阶段，而滑动平均相当于将最后的1000次抖动进行了平均，这样得到的权重会更加robust。

References

Course 2 Improving Deep Neural Networks by Andrew Ng

《TensorFlow实战Google深度学习框架》 4.4.3