UVA - 1279 Asteroid Rangers （动点的最小生成树）

题意，有n个匀速动点，求最小生成树的改变次数。

一句话总结：动态问题的一般做法是先求出一个静态的解，然后求出解发生改变的事件，事件按照时间排序，依次处理。

先求出最开始的最小生成树(MST)，当MST中的某条线段v长度被不在MST的线段u取代的时候，最小生成树才会发生变化，

具体来说，已经知道之前的MST，边按照长度排序，在这个时间点之前的瞬间，v一定是MST最长的边，u紧跟在v之后，在这个时间点之后u和v的位置交换了一下，

根据Kruskal算法，对于u和v之前的边没有影响，前面的边连完以后如果u的两个端点不在同一个连通分量里，那么u会被加入形成新的MST，否则MST不变。

根据边长的平方对时间的函数求出所有线段u和v长度相等且之后u更短的时间点，按照时间顺序排序，一旦满足上述条件，就修改MST。

为了维护MST需要维护一个MST到边的映射，为了判断新线段在不在MST中以及忽略旧边需要维护一个边到MST编号的映射。

求时间点时有解的三种情况：

一开始先对线段长度排过序，所以保证Lj>Li，

第一种情况是a=0，一个解，之后j更短。

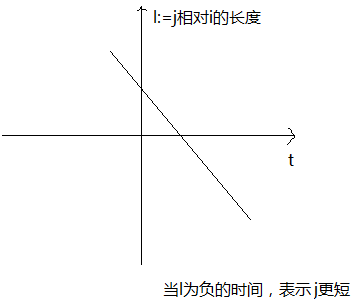
第二种情况是a<0，因为Lj>Li，所以只有大的那个是合法的，之后j更短。

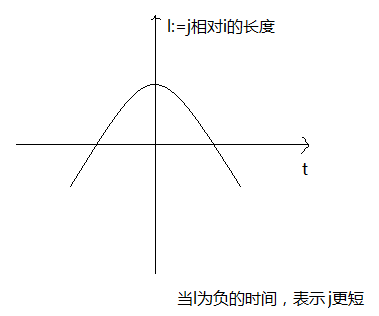
第三种情况，a>0，第一个解是j更短，第二个解是i更短。

#include<bits/stdc++.h>
using namespace std;

const double eps = 1e-;

struct Event
{
    double t;
    int u,v; //这个时间点以后u更短
    bool operator < (const Event& r) const {
        return t < r.t;
    }
};

vector<Event> events;
#define PB push_back
const int maxn = ;
const int maxl = maxn*(maxn-)>>;

struct Point
{
    double x,y,z,dx,dy,dz;
    void read(){ scanf("%lf%lf%lf%lf%lf%lf",&x,&y,&z,&dx,&dy,&dz); }
    Point operator - (const Point&r) { return {x-r.x, y-r.y, z-r.z, dx-r.dx, dy-r.dy, dz-r.dz}; }
}P[maxn];

#define squ(x)  ((x)*(x))

struct Seg
{
    double a,b,c;
    int u,v;
    void cal(int i,int j){
        u = i; v = j;
        Point t = P[i]-P[j];
        a = squ(t.dx) + squ(t.dy) + squ(t.dz);
        b = *(t.dx*t.x + t.dy*t.y + t.dz*t.z);
        c = squ(t.x) + squ(t.y) + squ(t.z);
    }
}L[maxl];

bool operator < (const Seg&x, const Seg&y) { return x.c < y.c; }

int lcnt;
int n;

//if equation has two roots, r1 < r2
int solveEqu(double a,double b,double c,double &r1,double &r2)
{
    if(fabs(a)<eps){
        if(fabs(b)<eps) return ;
        r1 = -c/b;
        return ;
    }
    double delta = b*b-.*a*c;
    if(delta<eps) return ;
    delta = sqrt(delta);
    if(a>){
        r1 = (-b-delta)/(.*a);
        r2 = (-b+delta)/(.*a);
    }else {
        r1 = (-b+delta)/(.*a);
        r2 = (-b-delta)/(.*a);
    }
    return ;
}

int pa[maxl];

int pos[maxl]; //map: Edge  to MST
int e[maxn]; //map: MST to Edge

void initUFS() { for(int i = ; i < n; i++) pa[i] = i; }
int Find(int x) { return x == pa[x]?x:pa[x]=Find(pa[x]); }

int main()
{
    //freopen("in.txt","r",stdin);
    int kas = ;
    while(~scanf("%d",&n)){
        for(int i = ; i < n; i++) P[i].read();
        events.clear(); lcnt = ;
        for(int i = ; i < n; i++){
            for(int j = i+; j < n; j++){
                L[lcnt++].cal(i,j);
            }
        }
        sort(L,L+lcnt);//ascending order

        for(int i = ; i < lcnt; i++){
            for(int j = i+; j < lcnt; j++){
                double r[];
                double a = L[j].a - L[i].a//j相对i的长度
                , b = L[j].b - L[i].b
                , c = L[j].c - L[i].c;

                int rcnt = solveEqu(a,b,c,r[],r[]);
                if(rcnt == ){
                    if(r[]>) events.PB({r[],j,i});
                }else if(rcnt == ){
                    if(a<){
                        if(r[]>) events.PB({r[],j,i});
                    }else {
                        if(r[]>) events.PB({r[],j,i});
                        if(r[]>) events.PB({r[],i,j});
                    }

                }
            }
        }
        sort(events.begin(),events.end());
        //DeBugEv
        initUFS();
        memset(pos,,sizeof(int)*lcnt);

        int idx = ;
        for(int i = ; i < lcnt; i++){
            int s1 = Find(L[i].u), s2 = Find(L[i].v);
            if(s1 != s2){
                pa[s1] = s2;
                e[pos[i] = ++idx] = i; //e[] 下标从1开始。0表不在MST中
                if(idx == n-) break;
            }
        }

        int ans = ;
        for(int i = ; i < events.size(); i++){
            Event &ev = events[i];
            if(pos[ev.v]&&!pos[ev.u]){
                initUFS();
                int old = pos[ev.v];
                for(int j = ; j <= idx; j++){
                    if(j == old) continue;
                    int s1 = Find(L[e[j]].u), s2 = Find(L[e[j]].v);
                    if(s1 != s2){ pa[s1] = s2; }
                }
                int s1 = Find(L[ev.u].u), s2 = Find(L[ev.u].v);
                if(s1 != s2){
                    ans++;
                    pos[ev.u] = old;
                    pos[ev.v] = ;
                    e[old] = ev.u;
                }
            }
        }
        printf("Case %d: %d\n",++kas,ans);
    }
    return ;
}