URAL题解三

URAL题解三

URAL 1045

题目描述：有\(n\)个机场，\(n-1\)条航线，任意两个机场有且只有一种方案联通。现有两个恐怖分子从\(m\)号机场出发，第一个人在机场安装炸弹，乘坐飞机，引爆炸弹，在另一个机场降落，然后到第二人做一样的事，轮流做，直到某个人做不到就输。一个机场炸了后，任何与它相连的航线都不复存在。问第一个人能不能赢，如果能，则输出他第一个要飞到的机场，如果不能则输出First player loses

solution
博弈论，输赢状态的搜索。
时间复杂度：\(O(n)\)

URAL 1046

题目描述：在平面上有一个多边形，顶点坐标为\(A_i\)(顺时针)，在多边形的每条边的外侧作一个点\(M_i\)，使得\(M_i\)与对应边的两个点组成一个等腰三角形(对应边为底边)，给出\(M_i\)和对应三角形顶角的角度\(\alpha _i\)，求\(A_i\)。

solution
一开始不知道等腰有什么用，下意识就想去几何关系了。后来才想到：如果把\(M_i\)看成圆心，腰看成半径，那对应边的两个点都在圆上，也就是说，这两个点可以通过绕着\(M_i\)旋转一定角度得到，而这个角度就是\(\alpha _i\)。列出两条方程，发现未知数都是一次方的，可以用高斯消元解出所有未知数。
时间复杂度：\(O((2n)^3)\)

URAL 1047

题目描述：有\(n+2\)个数，\(a_0, a_1, ..., a_{n+1}\), 当\(1 \leq i \leq n\)时，\(a_i=(a_{i-1}+a_{i+1})/2-c_i\)，给出\(a_0, a_{n+1}, c_i\)，求\(a_1\)。

solution
一开始我又蠢蠢地去推公式，想直接算出答案。后来从问的结果得到灵感：不是只要求\(a_1\)吗？如果我能将\(a_{n+1}\)与\(a_0, a_1\)的关系递推出来，问题就解决了。整理一下公式
\[a_i=2(a_{i-1}+c_{i-1})-a_{i-2}\]
把每个\(a_i\)都表示为\(a_i=pa_0+qa_1+m\)，最终就可以求出\(a_{n+1}\)，解出答案。
时间复杂度：\(O(n)\)

URAL 1048

题目描述：给出两个\(n\)位数，求两个数的和。

solution
高精度，只是要注意一定要输出\(n\)位。
时间复杂度：\(O(n)\)

URAL 1049

题目描述：给出\(10\)个数，求这\(10\)个数的乘积的因数个数的个位。

solution
设\(10\)个数的乘积的质因子有\(m\)个，每个质因子有\(s_i\)个，那么因数个数就是\(\prod_{i=1}^m (s_i+1)\)。所以把这\(n\)个数的质因子个数统计一下即可。
时间复杂度：\(O(10\sigma(10^4))\)

URAL 1050

题目描述：给出很多段落，每个段落进行如下处理：从左到右找出双引号(")对（不一定相邻），将前一个双引号变成两个左单引号(`)，将后一个双引号变成两个右单引号(')，如果不成一对，则删去单独的双引号。注意：(\)后面紧接着的非字母字符串中的双引号不作处理（即找双引号时将其忽略）。
输出最终的段落。

solution
本来想一边读入一边处理，后来发现这样太恶心了，干脆就将它们一次过全部读进来，再对不同段落，是否结束，是否忽略进行判断，这样就舒服多了。
时间复杂度：\(O(总长度)\)

URAL 1051

题目描述：有一个无限网格，其中有一个\(n*m\)的石头矩形，石头放在网格中。现在可以任选一个石头，如果它四相邻的某个格子上有石头，则它可以往该方向跳两格，吃掉（移走）越过的石头，任意时刻一个格子中不能有多个石头。问最终最少剩下多少个石头。

solution
假设\(n \leq m\)，当\(n<3\)时，显然答案是\((m+1)/2\)。
当\(n\)或\(m\)为\(3\)的倍数，则按下图进行处理：

所以答案是2.
当\(n>3\)且\(n\)不是\(3\)的倍数时，
先处理\(4*4, 5*5, 4*5\)

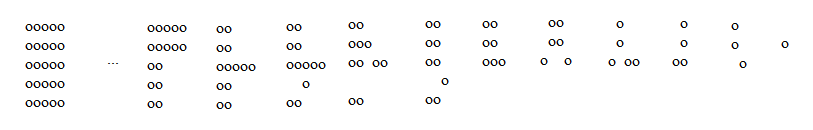
其它情况先三个三个地消除（像最上面第一个图），最后消成\(4\)或\(5\)行，然后用下面两个方法消列，最终变成\(4*4\)或\(5*5\)或\(4*5\)

所以答案是1.

URAL 1052

题目描述：在平面上有\(n\)个点，在平面上随意画一条直线，问最多穿过多少个点。

solution
两点确定一条直线，枚举两个点，再统计有多少个点在线上。
时间复杂度：\(O(n^3)\)