poj2479 Maximum sum

http://poj.org/problem?id=2479

题目大意：给定一组n个整数:a ={a1, a2，…，我们定义一个函数d(a)如下:

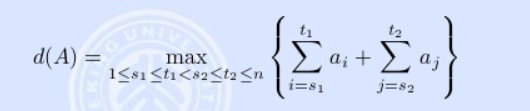
你的任务是计算d(A)。输入由T(<=30)测试用例组成。在输入的第一行中给出了测试用例(T)的数量。

每个测试用例包含两行。第一行是一个整数n(2<=n<=50000)。第二行包含n个整数:a1, a2，…,an。 ( | ai |  < = 10000)。为每个测试用例打印一行。该行应该包含整数d(A)。

 

也就是说求最大的子段和，给定一个数组，求数组里左子段的和加上右子段的和的最大值。

算法思想：动态规划，用left[i]表示第1个数到第i个数的最大子段和，用right[i]表示第i个数到第n个数的最大值。我们要求的就是left[i]+right[i+1]的最大值。

状态转移方程：

1） left[i]=max{left[i-1]+a[i],a[i]}  i=1,2,3,…;

2） right[i]=max{right[i+1]+a[i],a[i]}   i=n,n-1,…;

3） max=max{left[i]+right[i+1]}   i=n,n-1,…;

 #include <iostream>
 using namespace std;
 int MaximumSum(int a[],int n)
 {
     int sum = , max=INT_MIN;
     int *left, *right;
     left = new int[n + ];
     right = new int[n + ];
     left[] = -;
     right[n + ] = -;
     for (int i = ; i < n; i++)
     {
         sum = sum + a[i];
         if (sum > left[i-])left[i] = sum;
         else left[i] = left[i-];
         if (sum < )sum = ;//累加为负数时更新sum
     }
     sum = ;
     for (int i = n; i > ; i--)
     {
         sum = sum + a[i];
         if (sum > right[n+])right[i] = sum;
         else right[i] = right[i + ];
         if (sum < )sum = ;
         if (right[i] + left[i - ] > max)max = right[i] + left[i - ];//在此可直接计算max
     }
     delete []left;
     delete []right;
     return max;
 }
 int main()
 {
     int t, n;
     int array[];
     cin >> t;
     for (int i = ; i < t; i++)
     {
         cin >> n;
         for (int j = ; j <= n; j++)
         {
             scanf_s("%d", &array[j]);
         }
         cout << MaximumSum(array, n) << endl;
     }

     return ;
 }