机器学习(七) PCA与梯度上升法 (上)
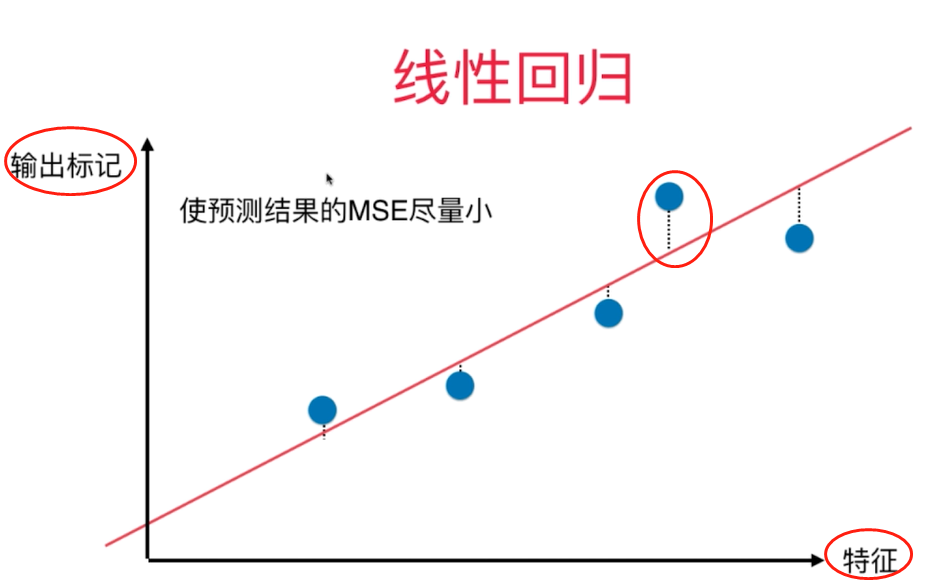
一、什么是PCA
主成分分析 Principal Component Analysis
一个非监督学的学习算法
主要用于数据的降维
通过降维,可以发现更便于人类理解的特征
其他应用:可视化;去噪

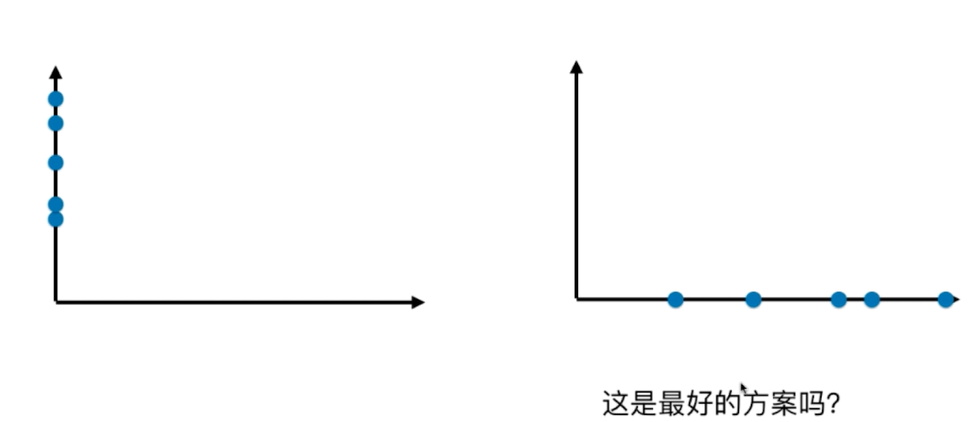
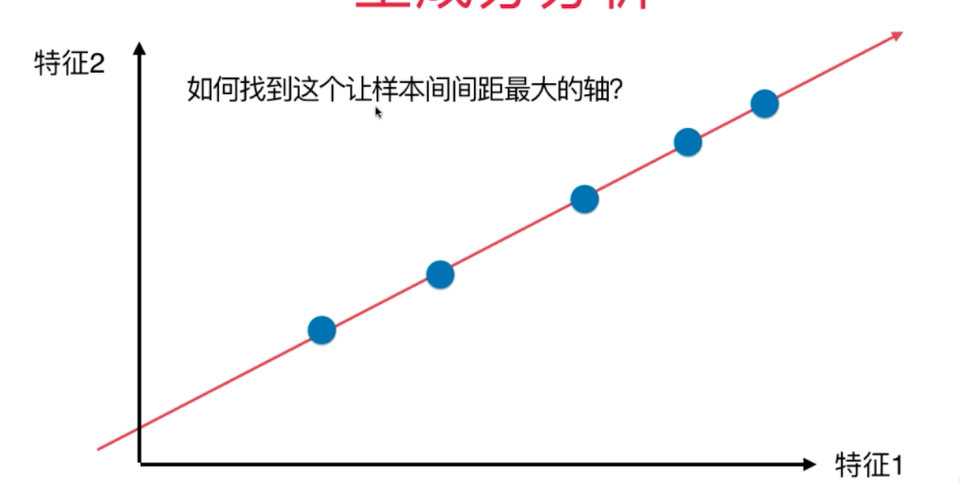

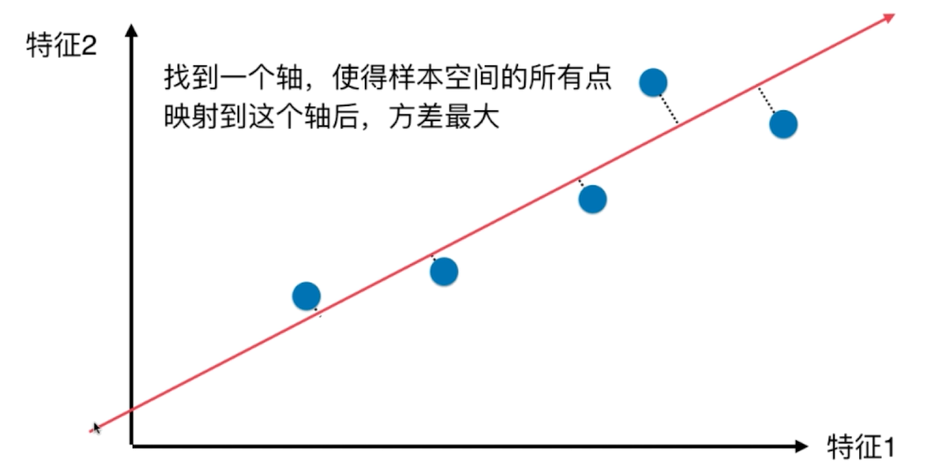
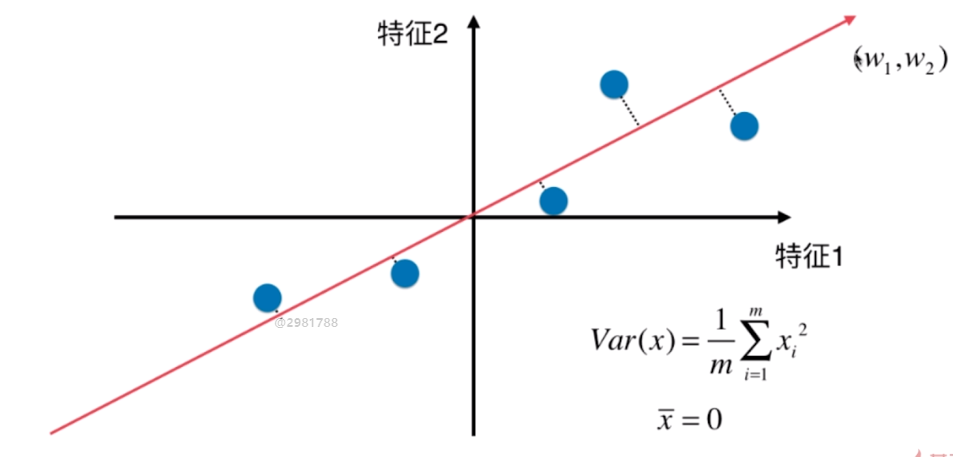
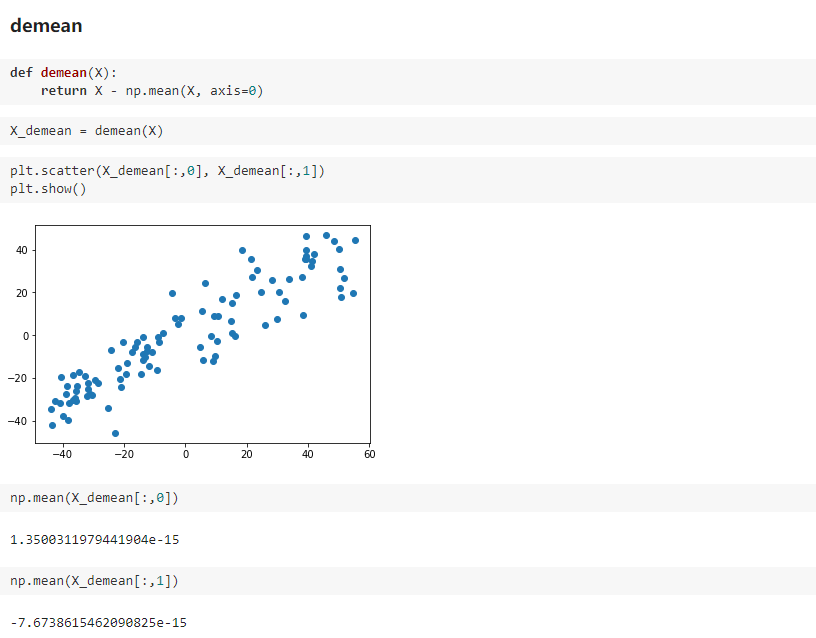
第一步:将样例的均值归零(demean)
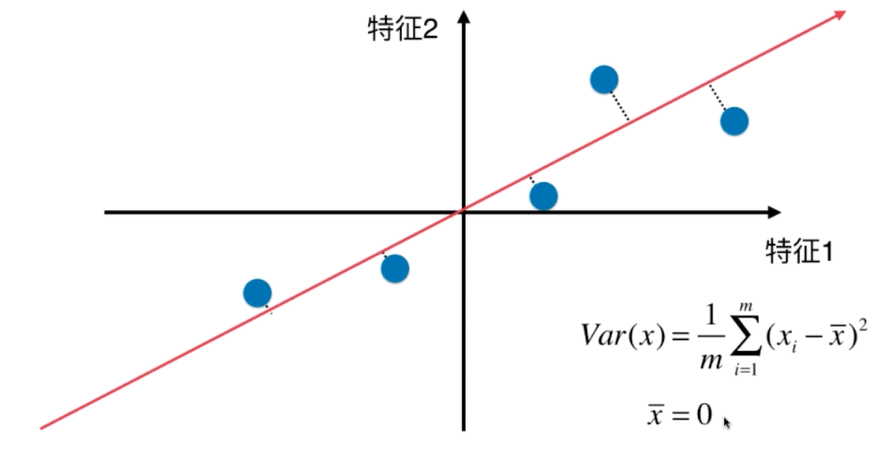

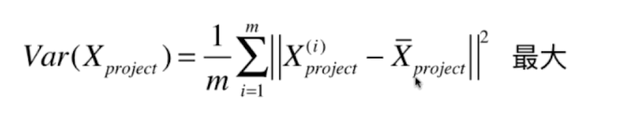
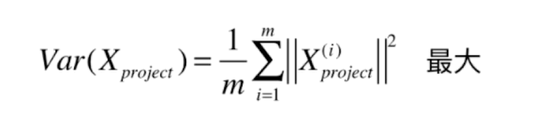
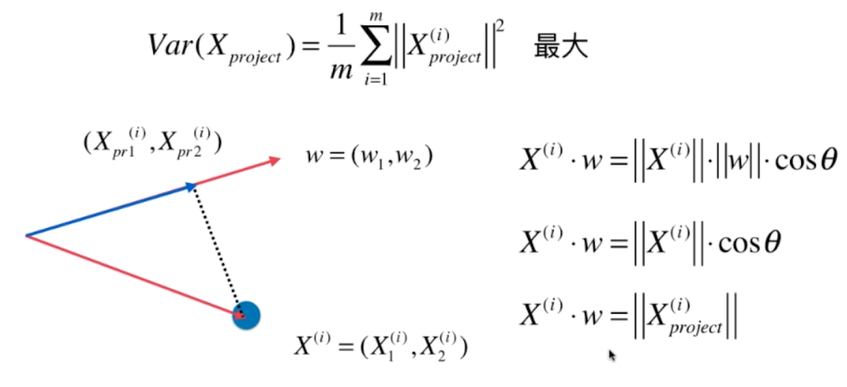
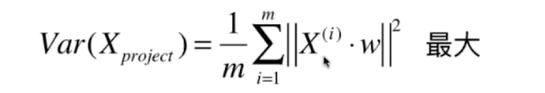


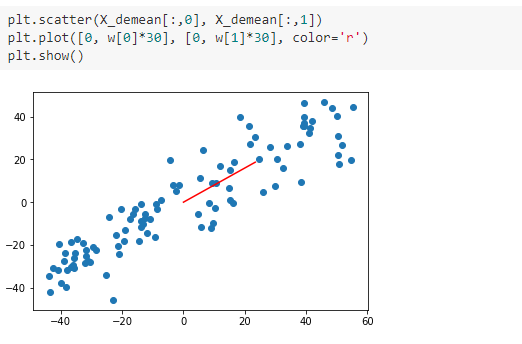
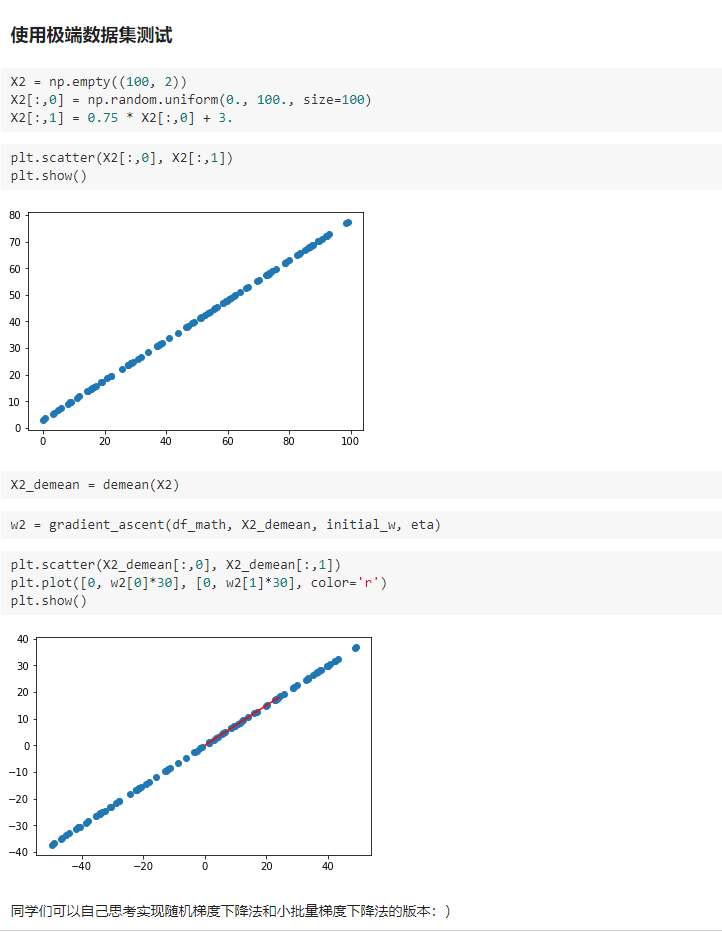
二、使用梯度上升法求解PCA问题
梯度上升法解决主成分分析问题

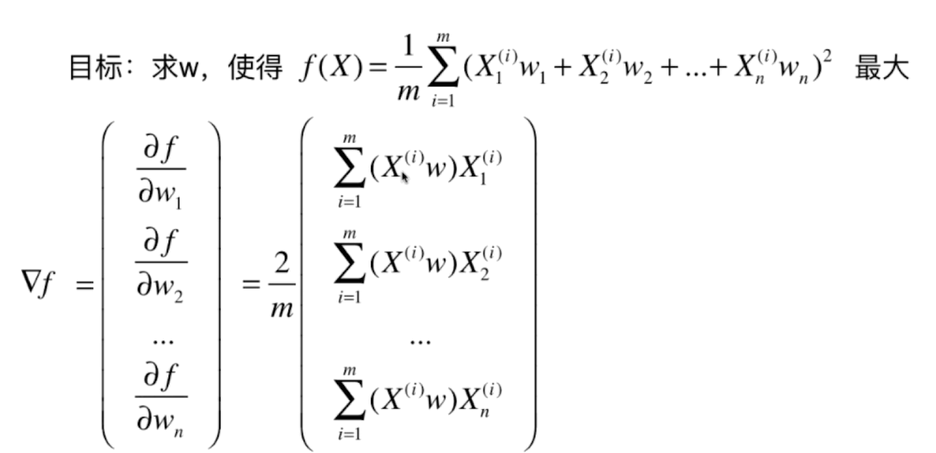
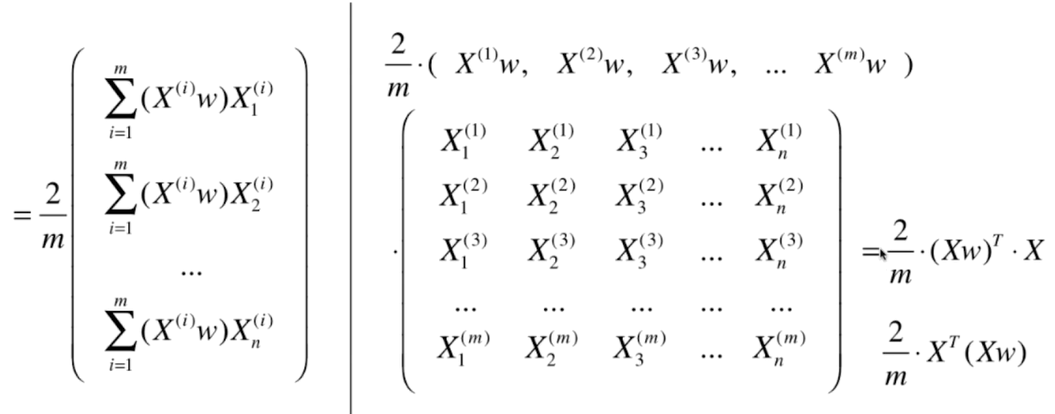
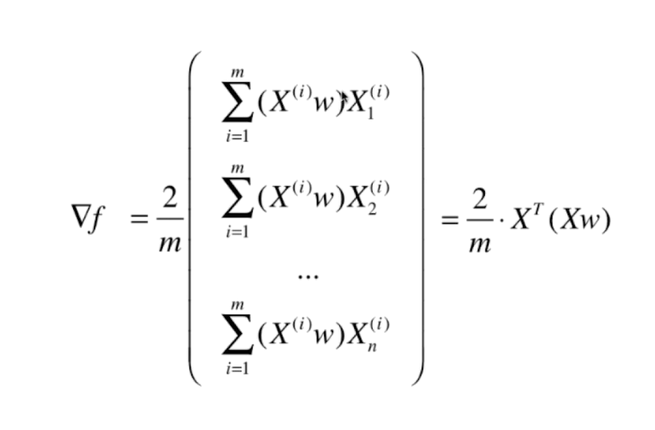
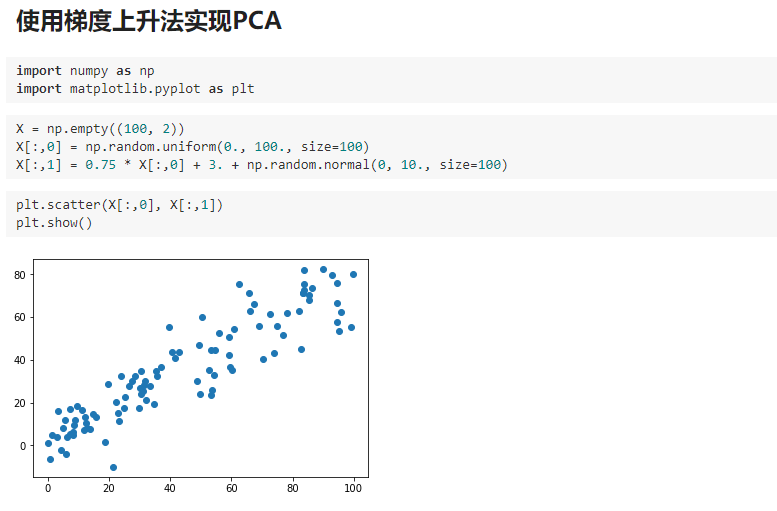
三、求数据的主成分PCA
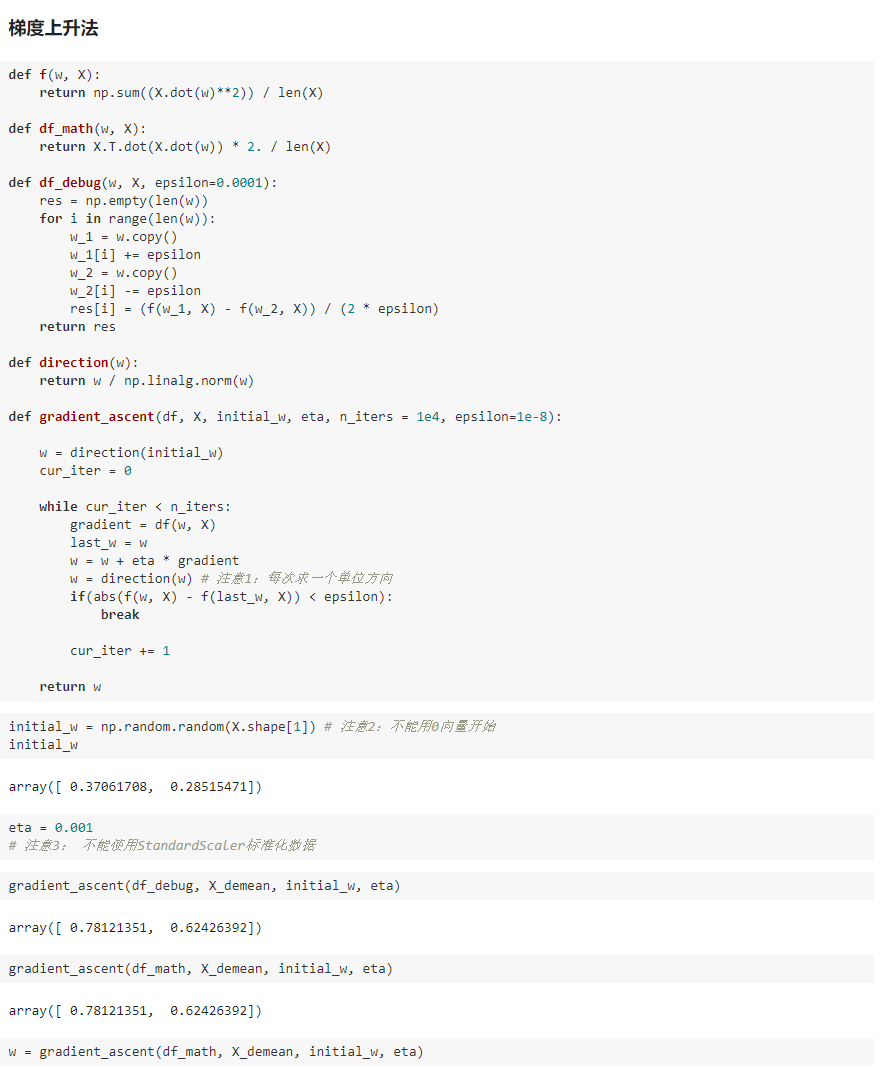
四、求数据的主成分 PCA
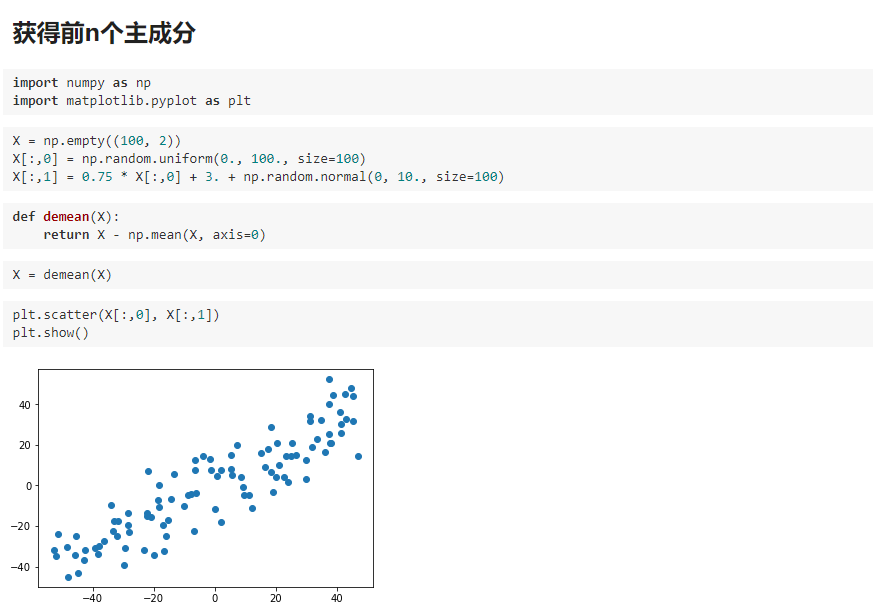
求数据的前 N 个主成分
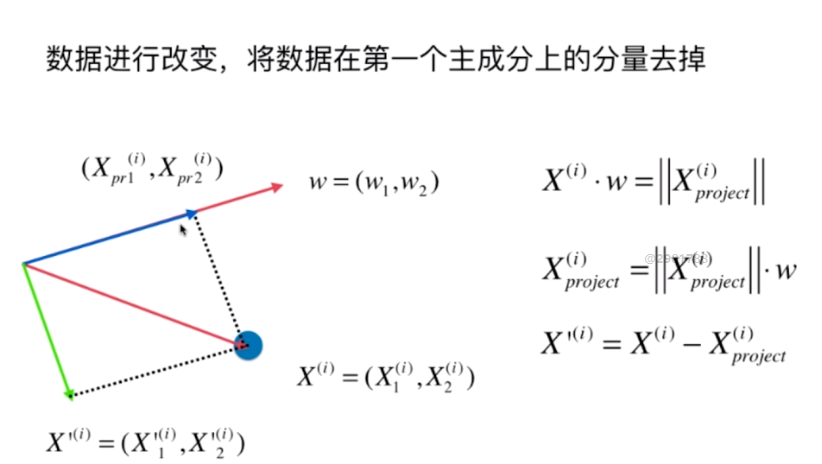
求出第一个主成分以后,如何求出下一个主成分?
数据进行改变,将数据在第一个主成分的分量去掉。

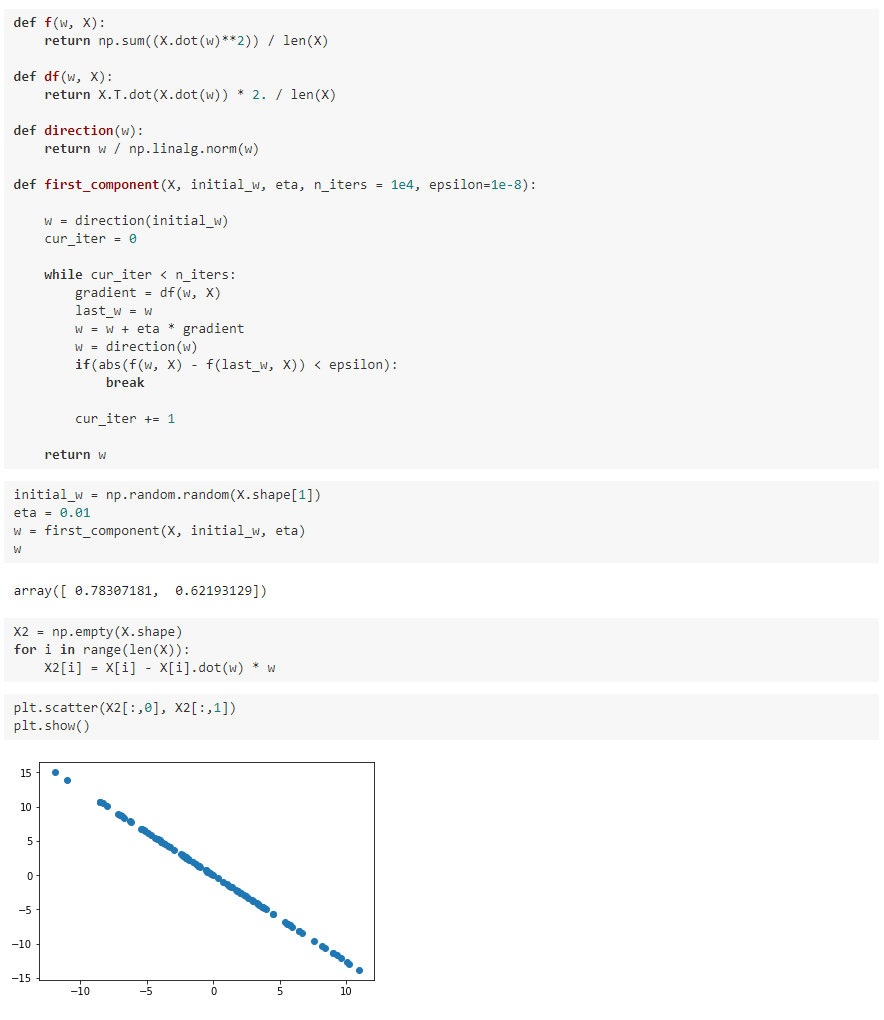
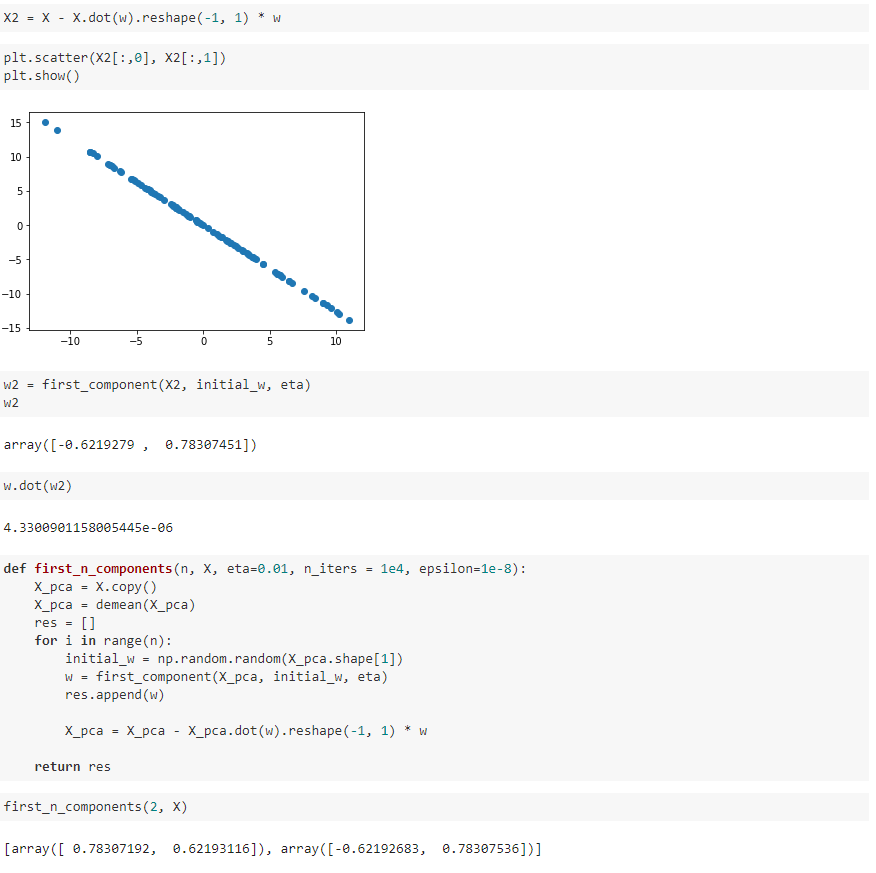
我写的文章只是我自己对bobo老师讲课内容的理解和整理,也只是我自己的弊见。bobo老师的课 是慕课网出品的。欢迎大家一起学习。
机器学习(七) PCA与梯度上升法 (上)的更多相关文章
- 机器学习(七) PCA与梯度上升法 (下)
五.高维数据映射为低维数据 换一个坐标轴.在新的坐标轴里面表示原来高维的数据. 低维 反向 映射为高维数据 PCA.py import numpy as np class PCA: def __ini ...
- 机器学习(4)——PCA与梯度上升法
主成分分析(Principal Component Analysis) 一个非监督的机器学习算法 主要用于数据的降维 通过降维,可以发现更便于人类理解的特征 其他应用:可视化.去噪 通过映射,我们可以 ...
- 4.pca与梯度上升法
(一)什么是pca pca,也就是主成分分析法(principal component analysis),主要是用来对数据集进行降维处理.举个最简单的例子,我要根据姓名.年龄.头发的长度.身高.体重 ...
- 第7章 PCA与梯度上升法
主成分分析法:主要作用是降维 疑似右侧比较好? 第三种降维方式: 问题:????? 方差:描述样本整体分布的疏密的指标,方差越大,样本之间越稀疏:越小,越密集 第一步: 总结: 问题:????怎样使其 ...
- 机器学习:PCA(使用梯度上升法求解数据主成分 Ⅰ )
一.目标函数的梯度求解公式 PCA 降维的具体实现,转变为: 方案:梯度上升法优化效用函数,找到其最大值时对应的主成分 w : 效用函数中,向量 w 是变量: 在最终要求取降维后的数据集时,w 是参数 ...
- 机器学习:PCA(高维数据映射为低维数据 封装&调用)
一.基础理解 1) PCA 降维的基本原理 寻找另外一个坐标系,新坐标系中的坐标轴以此表示原来样本的重要程度,也就是主成分:取出前 k 个主成分,将数据映射到这 k 个坐标轴上,获得一个低维的数据集. ...
- 机器学习:PCA(基础理解、降维理解)
PCA(Principal Component Analysis) 一.指导思想 降维是实现数据优化的手段,主成分分析(PCA)是实现降维的手段: 降维是在训练算法模型前对数据集进行处理,会丢失信息. ...
- 机器学习算法-PCA降维技术
机器学习算法-PCA降维 一.引言 在实际的数据分析问题中我们遇到的问题通常有较高维数的特征,在进行实际的数据分析的时候,我们并不会将所有的特征都用于算法的训练,而是挑选出我们认为可能对目标有影响的特 ...
- 机器学习算法的调试---梯度检验(Gradient Checking)
梯度检验是一种对求导结果进行数值检验的方法,该方法可以验证求导代码是否正确. 1. 数学原理 考虑我们想要最小化以 θ 为自变量的目标函数 J(θ)(θ 可以为标量和可以为矢量,在 Numpy 的 ...
随机推荐
- windows编译ffmpeg出现gcc is unable to create an executable file 的普通情况
近期有个朋友在编译ffmpeg的时候出现这个问题,他非常郁闷. 我就说,为什么我弄的时候就没问题呢??直接./configure +加上后面的參数 安全度过. 然后,我就想了,预计他的gcc的系统变量 ...
- Woody的Python学习笔记2
Python多行语句 Python语句中一般以新行作为语句的结束符.但我们能够使用斜杠(\)将一行的语句分为多行显示,例如以下所看到的: total = item_one+\ item_two + \ ...
- Linux下grub的配置文件
GRUB(统一引导装入器)是基本的Linux引导装入器. 其有四个作用,如下: 1.选择操作系统(如果计算机上安装了多个操作系统). 2.表示相应引导文件所在的分区. 3.找到内核. 4.运行初始内存 ...
- html单行、多行文本溢出隐藏
欢迎加入前端交流群来py:749539640 单行: div{/* 单行溢出隐藏 */ width: 150px; white-space: nowrap; overflow: hidden; tex ...
- Python之Linux下的virtualenv
在使用 Python 开发的过程中,工程一多,难免会碰到不同的工程依赖不同版本的库的问题: 亦或者是在开发过程中不想让物理环境里充斥各种各样的库,引发未来的依赖灾难. 此时,我们需要对于不同的工程使用 ...
- 从SQL注入谈数据访问层
什么是SQL注入? SQL注入就是应用程序的开发人员未预期的吧SQL语句传入到应用程序的过程,如果直接使用用户输入的值来构建SQL语句的应用程序是很可能会受到SQL注入攻击的.特别是基于浏览器的网络应 ...
- jqGrid添加删除功能(不和数据库交互)
jqGrid添加删除功能(不和数据库交互) 一.背景需求 项目中需要在前端页面动态的添加行,删除行,上下移动行等,同时还不和数据库交互.一直在用jqGrid展示表格的我们,从没有深入的研究过它,当然看 ...
- jq操作属性,元素,样式,事件
操作属性: 单个 $('选择器').attr('属性名','属性值'); 多个 $('选择器').attr({'属性名':'属性值','':''}); eg: $('#a1').attr('flag' ...
- 滚动监听 after选择器
一.如何实现滚动到一定位置将内容固定在页面顶部 window.onscroll=function(){ //滚动的距离,距离顶部的距离 var topScroll =document.body.scr ...
- SpringBoot(三) SpringBoot中的日志配置
SLF4J Spring Boot在所有内部日志中使用Commons Logging,但是默认配置也提供了对常用日志的支持,如:Java Util Logging,Log4J, Log4J2和Logb ...
